600√3.
Объяснение:
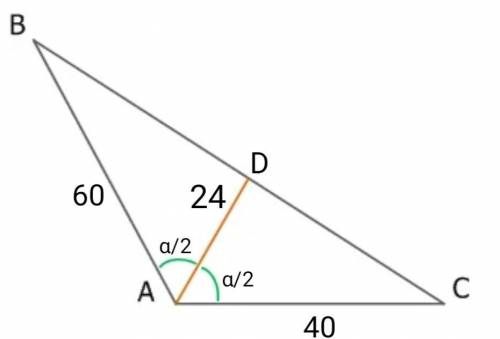
Пусть в данном треугольнике АВС ∠А = α, АD - биссектриса, АD = 24, AB = 60, AC = 40.
1) SABD = 1/2•AB•AD•sin(α/2) = 1/2•60•24•sin(α/2) = 720•sin(α/2).
SACD = 1/2•AC•AD•sin(α/2) = 1/2•40•24•sin(α/2) = 480•sin(α/2).
тогда SABC = SABD + SACD = 1200•sin(α/2).
2) С другой стороны,
SAВC = 1/2•AC•AВ•sinα = 1/2•40•60•sinα = 1200•sinα.
3) Составим равенство:
1200•sin(α/2) = 1200•sinα
sin(α/2) = sinα
sin(α/2) = 2•sin(α/2)•cos(α/2)
α - угол треугольника, тогда sin(α/2) ≠ 0,
1 = 2•cos(α/2)
cos(α/2) = 1/2, α/2 = 60°, α = 120°.
3) SAВC = 1200•sinα = 1200•sin120° = 1200°•sin(180° - 60°) = 1200•sin60° = 1200•√3/2 = 600√3.
18 см - первая сторона
12 см - вторая сторона
6 см - третья сторона
27 см - четвертая сторона
Объяснение:
Пусть первая сторона = х см, тогда:
2/3х см - вторая сторона (2/3 первой)
2/3х*0,5 = 1/3х см - третья сторона (50% второй)
х*1,5 = 1,5х = 15/10х = 3/2х см - четверная сторона (150% первой)
Составим уравнение:
х + 2/3х + 1/3х + 3/2х = 63
7/2х = 63
х = 63 : 7/2
х = 63 * 2/7
х = 18 (см) - первая сторона
18*2/3 = 12 (см) - вторая сторона
18*1/3 = 6 (см) - третья сторона
18*3/2 = 27 (см) - четвертая сторона
18+12+6+27 = 63 (см) - периметр 4-х угольника