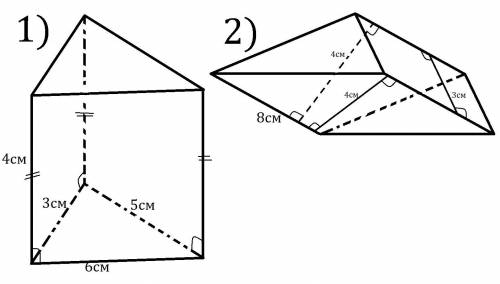
1)
Призма прямая, поэтому боковыми гранями будут прямоугольники. Одна их сторона это боковое ребро, а другая сторона это сторона основания. Найдём площадь боковой поверхности призмы как сумму площадей прямоугольников, которые составляют бок. пов.
S = 4см · 3см + 4см · 5см + 4см · 6см =
= 4см · (3см+5см+6см) = 4см · 14см = 56см².
ответ: 56см².
2)
Расстоянием между боковыми рёбрами призмы будет длина отрезка заключенного между боковыми рёбрами и лежащий на общем перпендикуляре. Боковые рёбра наклонной призмы это параллелограммы у которых мы знаем одну сторону (бок. реб.) и высоту проведённую к этой стороне (расстояние между бок. реб.), поэтому мы можем найти площадь параллелограмма. Площадь боковой поверхности найдём как сумму площадей параллелограммов, которые составляют бок. пов.
S = 8см · 3см + 8см · 4см + 8см · 5см =
= 8см · (3см + 4см + 5см) = 8см · 12см = 96см².
ответ: 96см².
Свойство пересекающихся хорд: точка пересечения хорд делит их на отрезки так, что произведение длин отрезков одной хорды равно произведению длин отрезков другой.
АО·ВО=СО·ДО.
АО=ВО=АВ/2=15 см.
Пусть ДО=х, тогда СО=х+40.
15·15=(х+40)·х,
225=х²+40х,
х₁=-45, (х<0 не подходит по смыслу задачи),
х₂=5.
СД=СО+ДО=х+40+х=5+40+5=50 см.
R=СД/2=25 см - такой ответ.