1) Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
2) Все 3 признака равенства треугольников:
а) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
б) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
в) Если 3 стороны одного треугольника соответственно равны 3-ем сторонам другого треугольника, то такие треугольники равны.
3) Треугольника называется равнобедренным, если 2 его стороны равны.
В равнобедренном треугольнике углы при основании равны.
4) Отрезок угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны называется биссектрисой треугольника. Биссектриса делит угол на 2 равные части.
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны называется медианой треугольника.
Перпендикуляр, проведенный из вершины треугольника к прямой, соединяющей противоположную сторону, называется высотой треугольника.
--------
Чертежи во вложениях



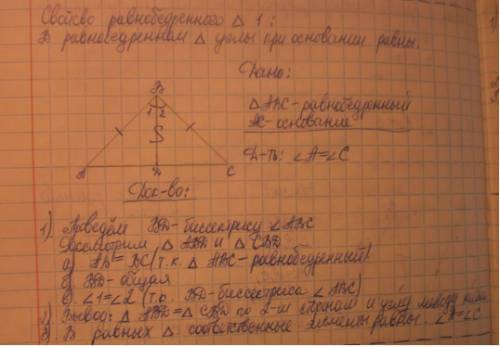
1. Равнобедренный треугольник - треугольник, у которо две стороны равны.
У такого треугольника углы при основании равны.
Биссектриса угла - это луч, делящий данный угол пополам.
Построение биссектрисы угла: 1) берем произвольный раствор циркуля и описываем дугу с центром в вершине угла так, чтобы она пересекала стороны угла
2) этим же раствором проводим дуги с вершиной в точках пересечения исходной дуги со сторонами. Через точку, где эти две новые дуги пересеклись, проводим прямую, которая прохдит и через вершину угла. Полученная прямая и будет биссектрисой угла.
Пусть меньший смежный угол равен х. Тогда другой будет равен 5х. По теореме о сумме смежных углов, получаем: 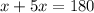
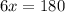
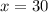 .
.
Мы нашли меньший угол. Теперь найдем больший: 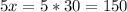
ответ: 30, 150.
ВС=2R·sin 2α;
OR=0.5BC=R·sin 2α/
OK=√(OC²-OK²)=√(R²-R²sin²2α)=Rcos2α.
AK=OA+OK=R+Rcos2α.
Площадь основания призмы: S=0,5·BC·AK=0,5·2Rsin2α·(R+Rcos2α)=
=Rsin2α·(R+Rcos2α).
ΔAOA1. tg2α=OA1/OA; OA1=R·tg2α. ОА1-высота призмы.
V=S·OA1=Rsin2α·(R+Rcos2α)·R·tg2α.
ответ: R³tg2α·sin2α(1+cos2α).