
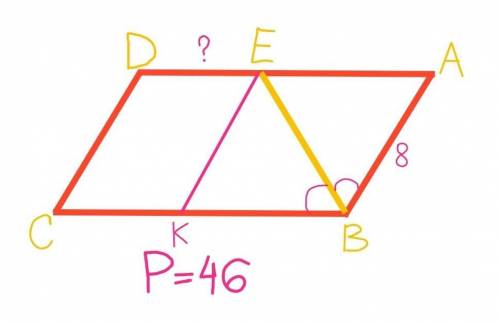
Объяснение:
Из точки Е проведем отрезок ЕК, параллельный АВ.
Противоположные стороны параллелограмма параллельны, тоесть СВ//DE => ЕА//КВ и DE//CK
Так как в четырехугольнике КЕАВ стороны попарно параллельны, следовательно КЕАВ – параллелограмм.
ВЕ – биссектриса угла КВА по условию и диагональ параллелограмма КЕАВ.
Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб.
Следовательно: КЕАВ – ромб
У ромба все стороны равны. Исходя из этого: ЕА=КВ=АВ=8 см.
СD=AB=8 так как противоположные стороны параллелограмма равны.
Р(АВСD)=АВ+ВС+CD+AD=AB+BK+KC+CD+DE+EA=8+8+KC+8+DE+8=32+KC+DE
Так как Р(ABCD)=46 см по условию, то получим уравнение:
32+КС+DE=46
KC+DE=14 см
Так как ЕК//АВ, а АВ//CD, то ЕК//CD;
DE//CK (доказано ранее);
Исходя из этого: CDEK – параллелограмм.
Противоположные стороны параллелограмма равны, тоесть DE=CK.
Тогда 2DE=14 см
DE=7 см
ответ: 7 см
Обозначим трапецию АВСD. М - точка пересечения диагоналей, угол АМD=90°. Проведем из вершины С параллельно ВD прямую до пересечения с АD в точке К. СК║ВD, АС при них - секущая, ⇒ соответственные ∠АСК=∠АМD=90°. Треугольник АСК прямоугольный, а так как DK=BC, его высота и площадь равна площади трапеции ABCD, S=0,5(AD+DK)•CH Высоту прямоугольного треугольника, проведенную из прямого угла, находят делением произведения катетов на гипотенузу. h=CH=АС•СК:АК. По т.Пифагора АК=√(AC²+CK²)=√(12²+16²)=20 см. Высота СН=12•16:20=9,6 см