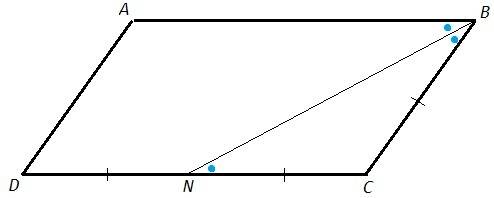
1) CN=CD/2=BC => △BCN - равнобедренный, углы при основании равны, ∠CBN=∠CNB
∠ABN=∠CNB (накрест лежащие при AB||CD)
∠ABN=∠CBN, BN - биссектриса ∠ABC (делит угол на два равных)
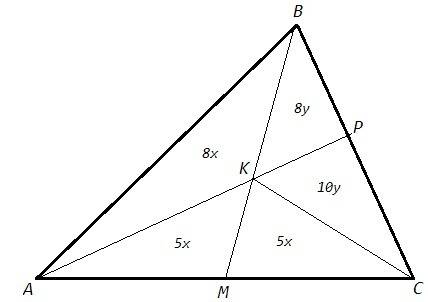
2) Площади треугольников с равной высотой относятся как их основания. Обозначим площади ABK=8x, AKM=MKC=5x, ACK=10x. Площади треугольников с равным основанием относятся как их высоты. Высоты треугольников ABK и ACK относятся как 8:10. Следовательно площади BKP и CKP относятся как 8:10. Обозначим площади BKP=8y, BKC=18y. Площади BKC и MKC относятся как 8:5.
S(BKC)/S(MKC) =18y/5x =8/5
S(BKP)/S(AKM) =8y/5x =8/5 * 4/9 =32/45
Или по теореме Менелая:
CP/PB *BK/KM *MA/AC =1 <=> CP/PB *8/5 *1/2 =1 <=> CP/PB=10/8
CM/MA *AK/KP *PB/BC =1 <=> AK/KP *8/18 =1 <=> AK/KP=18/8
Площади треугольников с равным углом относятся как произведения сторон, заключающих равные углы.
S(BKP)/S(AKM) =BK*KP/AK*KM =8/5 *8/18 =32/45
Задано Вершини трикутника ABC A(-5,1), B(3,-2), C(3,4).
Знайти:
1) Координати описаного кола. Это задание надо, скорее всего, понимать так: найти уравнение окружности, описанной около треугольника АВС.
Для этого надо определить координаты центра этой окружности и найти её радиус.
Решение возможно по нескольким вариантам.
Вот один из них.
Центр описанной окружности находится как точка пересечения серединных перпендикуляров сторон треугольника.
Есть формула, по которой сразу определяется уравнение серединного перпендикуляра по координатам вершин:
(x_1-x_2 )(x-(x_1+x_2)/2)+(y_1-y_2 )(y-(y_1+y_2)/2)=0.
Находим уравнение серединного перпендикуляра к стороне АВ.
Подставим координаты вершин А и В.
(-5-3)(x – ((-5+3)/2) + (1-(-2))(y – (1+(-2))/2) = 0,
-8(x + 1) + 3(y + (1/2)) = 0,
-8x – 8 + 3y + (3/2) = 0, умножим на (-2) и получаем уравнение:
16х – 6у + 13 = 0.
Второй перпендикуляр определяется просто, так как сторона ВС, имеющая точки с одинаковыми абсциссами, - это вертикальный отрезок прямой х = 3 между ординатами у = -2 и у = 4.
Середина её равна у = (-2+4)/2 = 1.
Значит, серединный перпендикуляр к стороне ВС – это горизонтальная прямая у = 1.
Находим их точку пересечения, подставив в уравнение первой прямой значение у = 1:
16х – 6*1 + 13 = 0, отсюда х = -7/16.
Получены координаты центра описанной окружности: О((-7/16); 1).
Далее надо найти радиус окружности.
Он равен расстоянию от центра окружности до любой вершины.
Находим R = OA = √((-5-(-7/16))² + (1-1)²) = 73/16 = 4,5625.
ответ: уравнение окружности (x + (7/16))² + (y – 1)² = (73/16)².
2) косинус кута BAC.
Находим векторы АВ и АС.
AB = {Bx - Ax; By - Ay} = {3 – (-5); -2 - 1} = {8; -3},
AC = {Cx - Ax; Cy - Ay} = {3 – (-5); 4 - 1} = {8; 3}.
Модули векторов равны:
|AB| = √(ABx2 + ABy2) = √(82 + (-3)2) = √(64 + 9) = √73,
|AC| = √(ACx2 + ACy2) = √(82 + 32) = √64 + 9 = √73.
ответ: cos(AB_AC) = (8*8 + (-3)*3)/(√73*√73) = 55/73 ≈ 0,7534.
Угол А равен 0,7175 радиан или 41,1121 градуса.
3) Координати точки D, яка ділить відрізок BC у відношенні до 2:3.
Для этого задания применяется формула:
x(D)=(x(B) + λ*x(C))/(1 + λ), где λ – отношение длин отрезков.
Получаем: x(D)=(3 + (2/3)*3)/(1 + (2/3)) = 3.
y(D)=(-2 + (2/3)*4)/(1 + (2/3)) = 2/5 = 0,4.
ответ: точка D(3; 0,4).
Проведем окружность с центром B и радиусом равным стороне квадрата. Т.к. ∠AEC=1/2∠ABC (т.е. ∠AEC равен половине центрального угла), то ∠AEC - вписанный, т.е. точка E лежит на окружности. Значит BC=BE как радиусы. Т.е. треугольник BCE - равнобедренный, и значит ∠CBE=180°-2·75°=30°.