Дано :
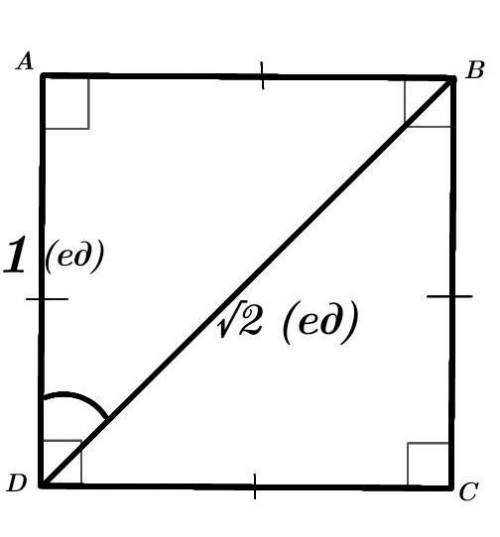
Четырёхугольник ABCD — квадрат.
AD = 1 (ед).
BD — диагональ = √2 (ед).
Найти :
соs(∠BDA) = ?
Квадрат — четырёхугольник, всё стороны которого равны, а все углы прямые.
Рассмотрим прямоугольный ∆ABD.
Косинус острого угла прямоугольного треугольника — отношение прилежащего катета к гипотенузе.
В нашем случае катет, прилежащий к ∠BDA — AD, а гипотенуза — BD (так как лежит против прямого угла).
То есть —
cos(∠BDA) = AD/BD
cos(∠BDA) = 1 (ед) / √2 (ед)
cos(∠BDA) = 1/√2
Или —
cos(∠BDA) = (√2)/2 (одно и тоже).
(√2)/2.
x-первая сторона
2x - вторая сторона
(2x-12)- третья сторона
63-периметр
5=75
x=15
наибольшая сторона треугольника 2x => 2*15=30
ОТВЕТ: 30
Возьмём меньшую сторону за x, Тогда большая сторона будет равняться 2x, а третья сторона 2x-12. Составим уравнение:
2x + x +2ч - 12 = 63
5x = 63 + 12 = 75
x = 15 см. - это меньшая сторона.
А большая = 15 * 2 = 30 см.