Объяснение:
Смежные и вертикальные углы. Перпендикулярные прямые
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. углы АОВ и ВОС смежные.
Геометрия ГИА, Сумма смежных углов равна 180°
Сумма смежных углов равна 180°
Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
Геометрия ГИА, Вертикальные углы равны
Вертикальные углы равны
Рис.2
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
Геометрия ГИА, Прямые АС и BD перпендикулярные
Рис.3
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
Геометрия ГИА, АН — перпендикуляр к прямой
АН — перпендикуляр к прямой
Рис.4
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Геометрия ГИА, Чертежный угольник
Чертежный угольник
Рис.5
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».
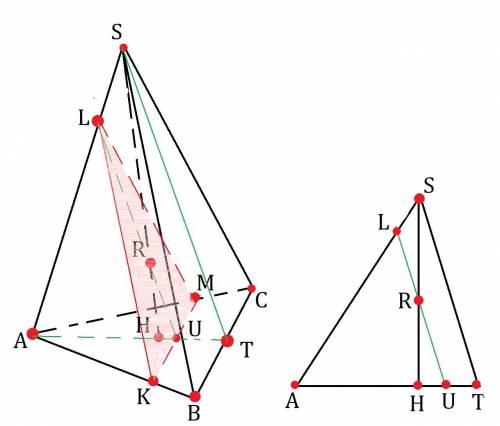
a) K, L, M ∈ α; α║(SBC)
KL║BS; KM║BC; ML║CS как линии пересечения двух параллельных плоскостей с одной общей.
SH⊥(ABC); AT⊥BC; H∈AT как центр правильного треугольника лежащий на медиане. AH:HT=2:1 по свойству пересечения медиан.
LU⊥KM ⇒ KU=UM ⇒ U∈AT ⇒ LU⊂(AST) ⇒ LU∩SH
Рассмотрим плоскость AST.
LU║ST как линии пересечения двух параллельных плоскостей с (AST).
AK:KB=AL:LS=5:1 по теореме о пропорциональных отрезках.
AU:UT=AL:LS по теореме о пропорциональных отрезках.
Как уже известно AH:HT=2:1. Пусть AU=5x; UT=x ⇒AT=6x ⇒ AH=4x; HT=2x ⇒ HU=2x-x=x.
ΔSHT~ΔRHU по 3 углам (1 общий остальные равны как соответственных угла при параллельных прямых).
Значит SH:RH=HT:HU=2:1. Пусть SH=2y; RH=y ⇒ SR=2y-y=y ⇒ SR=y=RH
То есть плоскость делит высоту пополам.
б) AT=AB*sin 60°=(15+3)*√3/2=9√3.
ΔAST~ΔALU по 3 углам (1 общий остальные равны как соответственных угла при параллельных прямых).
Значит AL:AS=LU:ST=6:5.
HT=1/3 *9√3=3√3 т.к. AH:HT=2:1
SH=13 ⇒ ST=√(169+27)=14 ⇒ LU=5/6 *14=35/3.
ΔAKM~ΔABC по 3 углам (1 общий остальные равны как соответственных угла при параллельных прямых).
Значит KM:BC=AK:AB=5:6 ⇒ KM=5/6 *18=15.
Как было указано в начале LU⊥KM ⇒ S=1/2* 15*35/3=175/2=87,5
ответ: 87,5.