1.Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Решение.
Треугольники HOBи KOB равны, т. к. являются прямоугольными с общей гипотенузой и равными катетами, значит, HB=KB=3
PABC=AC+CB+AH+HB=2CB+2HB=16+6=22
ответ: 22
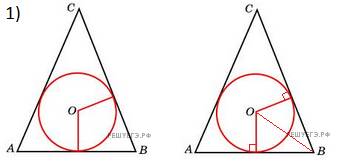
2. В равнобедренный треугольник АВС с основанием ВС вписана окружность. Она касается стороны АВ в точке М. Найдите радиус окружности, если АМ = 8 и ВМ = 12.
S=1/2p*r
r=2s/p
Т.к треугольник ABC-равнобедренный, то AB=AC=30
По свойству касательных: АМ=АЕ=8, СЕ=СК=12,ВМ=КВ=12,значит ВС=24
По формуле Герона S треугольник = в корне p(p-a)(p-b)(p-c)
1.3) Теорема. От любой данной точки можно отложить направленный отрезок, равный данному, и притом – только один.
Если данный направленный отрезок – нулевой, то утверждение теоремы очевидно. Пусть отрезок – ненулевой. Проведем через точку С прямуюl, параллельную (АВ). Направленный отрезок, который нам надо отложить, обязан лежать на этой прямой (ибо он коллинеарен ) и иметь длину |АВ|. От точки С можно отложить ровно два таких отрезка – обозначим изи(рис. 4), причем(почему?). В силу (Н4) если, то, а если, то. Таким образом, в обоих возможных случаях существует ровно один искомый отрезок, что и требовалось доказать.
(1.4) Теорема. Все направленные отрезки разбиваются на непересекающиеся классы отрезков таким образом, что любые два отрезка из одного класса равны между собой, а из разных классов – не равны.
Зафиксируем произвольную точку О, и для каждого направленного отрезка , исходящего из этой точки, обозначим через К() класс (т.е., совокупность) всех равных ему отрезков. При этом каждый направленный отрезок попадет ровно в один из таких классов, а именно, в класс равного ему направленного отрезка, отложенного от точки О. Поскольку любые два отрезка из одного и того же класса К() равны отрезку, они равны и между собой (теорема 1.2). Теперь допустим, что нашлись равные отрезкиК() иК(). Но тогда===, откуда по той же теореме 1.2=. Таким образом, если два отрезка равны, то они лежат в одном классе, то есть отрезки из разных классов не могут быть равными. В частности, это означает, что разные классы не могут пересекаться.
2)AB+AC=BC, т.к. 10,7+6,4=17,1