

ответ: Расстояние между центрами окружностей = 12
Объяснение: Смотрите рисунок.
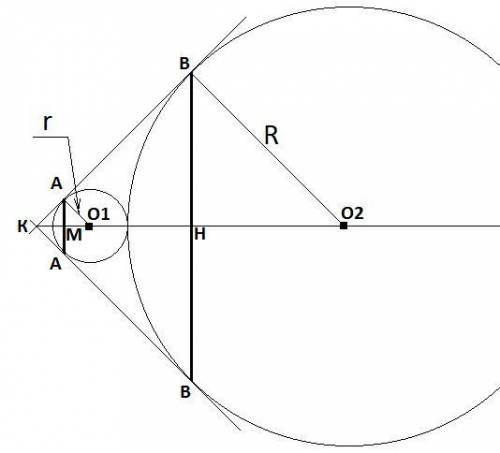
К – точка пересечения касательных. Угол К – прямой. КО2 – биссектриса угла К. А и А, а так же В и В – точки касания окружностей касательных. АА и ВВ – хорды окружностей, пересекают биссектрису в точках М и Н соответственно. О1 и О2 – центры окружностей. На рисунке видно, что расстояние между центрами окружностей О1О2 = r + R. Найдем r. АО1 параллельна КА. Т.к КО1 – биссектриса угла К, то АА перпендикулярна КО1. Следовательно ∠КАМ = ∠МАО1 = 90/2 = 45° Т.к. ∠АМО1 = 90°, то ∠АО1М = 180 – 90 – 45 = 45°. Таким образом, ΔАМО1 – равнобедренный и О1М = АМ = (2√2)/2 = √2. Следовательно, r = √{(√2)² + (√2)²} = √4 = 2. Аналогично для R: О2Н = ВН = (10√2)/2 = 5√2. Тогда R = √{(5√2)² +(5√2)²} = √(25*2) + (25*2) = √100 = 10. Расстояние между центрами окружностей = 2 + 10 = 12
-Чому дорівнює сума кутів трикутника? 180 градусів
- Який кут називається зовнішнім? Зовнішній кут — це кут, суміжний з кутом даного трикутника.
- Чому дорівнює градусна міра зовнішнього кута? Сумі градусних мір двох інших внутрішніх кутів.
- Яка сторона трикутника є найбільшою? Та, яка лежить навпроти найбільшого кута.
- Нерівність трикутника.
- Який трикутник є прямокутним? Той, у якого кут 90 градусів.
- Як називаються сторони прямокутного трикутника? Катети та гіпотенуза.
- Чому дорівнює сума його гострих кутів? 90 градусів
- Чому дорівнюють кути рівнобедреного прямокутного трикутника? 45,45,90
- Ознаки рівності прямокутних трикутників
якщо дві сторони та кут між ними одного трикутника дорівнює двом сторонам а куту між ними іншого, то ці трикутники рівні.
якщо сторона та два прилеглих до неї кути одного трикутника рівні стороні та двом прилеглим до неї кутам іншого, то ці трикутники рівні
якщо три сторони одного трик рівні трьом сторонам іншого, то ці трик рівні.
- Властивість катете, що лежить напроти кута 30. Той катет дорівнює половині гіпотенузи.
Де знайти завдання 3?