Основи двох рівнобедренних трикутників із рівними гострими кутами при вершині дорівнюють 15см і 5 см. В одному з трикутників бічна сторона дорівнює 7см.Знайдіть периметр другого трикутника

👇

Открыть все ответы

Ответ:

Krisitnka

07.09.2020

Смотрите рисунок к задаче, который приложен к ответу. На рисунке есть все построения, описанные в задаче, а именно: $\triangle CDE$ с прямым углом $\angle C = 90^{\circ}$ , EF — биссектриса $\angle E$ , CF = 13

, FG — искомый отрезок.
==========
Решение:
Докажем, что $\triangle CEF = \triangle EFG$ .
1) Так как

— биссектриса, то $\angle GEF = \angle CEF$ (биссектриса

делит $\angle E$ на два равные угла).
2) $\angle C =\angle FGE = 90^{\circ}$ (это следует из условия: так как $\triangle CDE$ прямоугольный, то и $\angle C = 90^{\circ}$ ; так как

— расстояние от

до

, то $\angle FGE = 90^{\circ}$ ).
3) Так как $\angle C =\angle FGE$ и $\angle GEF = \angle CEF$ , то и третий угол первого треугольника равен третьему углу второго треугольника: $\angle GFE = \angle EFC$ . Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так:
$\angle C + \angle CFE + \angle CEF = 180^{\circ} \\ 
\angle FGE + \angle GEF + \angle GFE = 180^{\circ}$
Отсюда:
$\angle CFE = 180^{\circ} - (\angle C + \angle CEF)\\ 
\angle GFE = 180^{\circ} - (\angle FGE + \angle GEF)$
Суммы в скобках в обоих уравнениях равны (так как, как я уже отмечал выше, углы, составляющие те суммы, равны), а значит равны и разности в обоих уравнениях, а значит $\angle CFE = \angle GFE$ .

3) Сторона

является для обоих треугольников общей.
Собранных сведений достаточно, чтобы заключить, что $\triangle CEF = \triangle EFG$ (второй признак равенства треугольников — по стороне и двум прилежащим к ней углам (

— сторона, а $\angle GEF = \angle CEF \,\,\,\, \angle GFE = \angle EFC$ — два прилежащих угла)).
Раз треугольники равны, то и все их их соответственные элементы равны. Видим, что искомой стороне

соответствует

, тогда:

ответ: 13.
=========
ответ можно проверить, геометрически (линейкой) измерив искомый отрезок

. Смотрите второй рисунок.

Впрямоугольном треугольнике cde с прямым углом с проведена биссектриса ef,причем fc=13 см. найдите р

4,6(21 оценок)

Ответ:

olga180982

07.09.2020

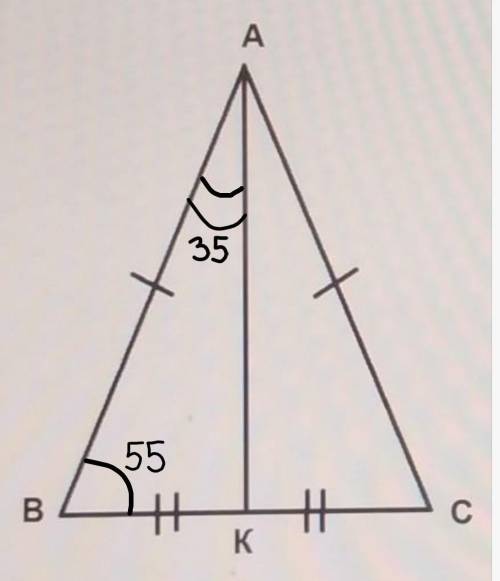
Дано:

AB = AC

угол BAK = 35°

BC = 10 см

ВК = KC

угол ABC = 55°

Найти:

ВК, угол KAC, угол BAC, угол AKB, угол ACB

ВС=ВК+КС, так как ВК=КС по условию, то ВК=ВС÷2. ВС=10 см по условию, тогда ВК=10÷2=5 см.

Так как АВ=АС по условию, то ∆АВС – равнобедренный с основанием ВС.

Углы при основании равнобедренного треугольника равны, то есть угол АСВ=угол АВС=55°

Так как ВК=КС, то АК – медиана проведенная к ВС.

Медиана, проведённая к основанию равнобедренного треугольника, так же является биссектрисой и высотой. Следовательно АК – биссектриса, тогда угол КАС=угол ВАК=35°, угол ВАС=угол ВАК*2=35°*2=70°. И угол АКВ=90°.

ответ: 5 см, 35°, 70°, 90°, 55°.