1. Дано: КМРТ - трапеция, КМ=РТ, КТ=14 дм, МР=8 дм. МН - высота, МН=4 дм. Найти КМ.
Решение: проведем высоту РС.
МР=СН=8 дм.
ΔКМН=ΔРСТ по катету и гипотенузе, КН=СТ=(14-8):2=3 дм.
Рассмотрим ΔКМН - прямоугольный, КН=3 дм, МН=4 дм, значит КМ=5 дм (египетский треугольник).
ответ: 5 дм.
2. Дано: КМСТ - прямоугольник, Р=56 см, КТ-МК=4 см. Найти МТ.
Решение: МК+КТ=56:2=28 см. Пусть КТ=х см, тогда МК=х-4 см.
Составим уравнение: х+х-4=28; 2х=32; х=16.
КТ=16 см; МК=16-4=12 см. Тогда по теореме Пифагора
МТ=√(16²+12²)=√(256+144)=√400=20 см.
(или просто: МТ=20 см, т.к. МК:КТ=12:16=3:4; МКТ - египетский треугольник)
ответ: 20 см.

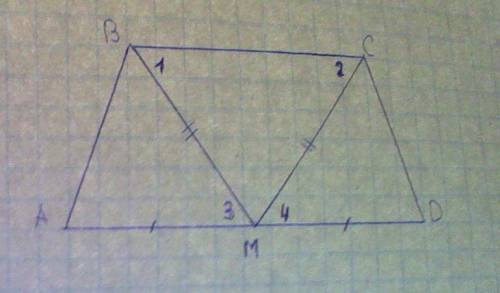
Смотри на рисунок
1)т.к ABCD трапеция, то BC перпендикулярно AD => угол 1= углу3 (накрест лежащие)
и угол 2=углу 4 (накрест лежащие)
2) M - равноудалена от B и С => MB=MC=> треугольник BMC- равнобедренный
=>угол 1=углу2
3) угол1=углу3 и угол2=углу4, а угол1=углу2 => угол3=углу4
4) в треуг. ABM и треуг. DCM:
а)BM=CM
б)AM=MD (M - серед AD)
в)угол3=углу4
5)треуг. ABM = треуг. DCM (по 2 сторонам и углу между ними) => AB=CD
6)AB=CD => трапеция равнобедренная