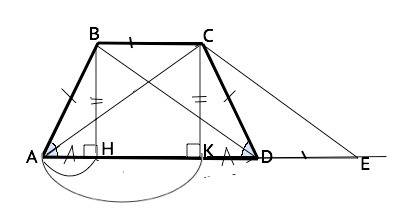
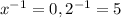Отсюда АН=(АD-BC):2
Проведем из С прямую параллельно диагонали , ВD до пересечения с продолжением АD в точке Е. DE║BC⇒CEDВ параллелограмм, DE=BC
АЕ=АD+BC
Треугольник АСЕ равнобедренный, его высота СК - медиана⇒
АК=АЕ:2, как и НD=АК=( АD+BC):2
----------
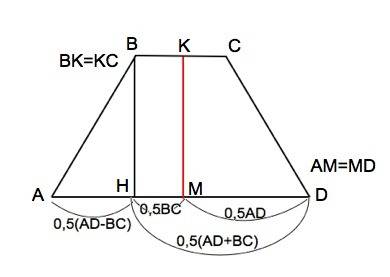
Рисунок второго приложения проще и не нуждается в особых комментариях.
Маловато ...
Четырехугольник (не только трапецию) можно описать около окружности тогда и только тогда, когда суммы его противоположных сторон равны. В данном случае в трапеции сумма боковых сторон равна сумме его оснований. Следовательно полупериметром трапеции можно считать либо сумму боковых сторон, либо сумму оснований. В нашем случае нам нужна сумма оснований. Обозначим ее за р. Теперь есть формула для вписанной в четырехугольник (не только трапеция!) окружности
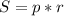
Здесь S - площадь трапеции, r - радиус вписанной окружности, р - полупериметр.
Остается только воспользоваться этой формулой
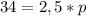
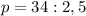
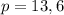
Как уже отмечали, полупериметр равен сумме оснований трапеции.
ответ: 13,6
![\frac{\sqrt[3]{x}*\sqrt[6]{x}}{\sqrt{x^3}}=\frac{x^{\frac{1}{3}}*x^{\frac{1}{6}}}{x^{\frac{3}{2}}}](/tpl/images/0154/9545/2fac9.png)
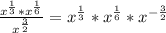
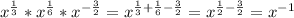
В случае, если х=0,2, то