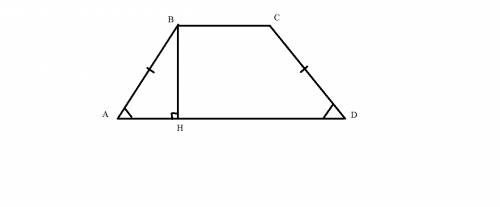
Извини за небрежность рисунка, рисование мне всегда давалось нелегко.
Угол ВАН равен 60 градусов. Проведем высоту. Угол АВН равен 30 градусов, значит, АН равна половине гипотенузы, равна 0,5. Такую же операцию нужно проделать с другой боковой стороной. Итого, получается, что меньшее основание равно 2,7-1=1,7
Средняя линия равна полусумме оснований, равна (2,7+1,7)/2=2,2.
Площадь трапеции равна высоте, умноженной на среднюю линию. Высота равна (по теореме Пифагора) корню из 0,75=0,5 корня из 3. Значит, площадь равна 1,1 * корень из 3
ответ: S=1.1 * корень из 3
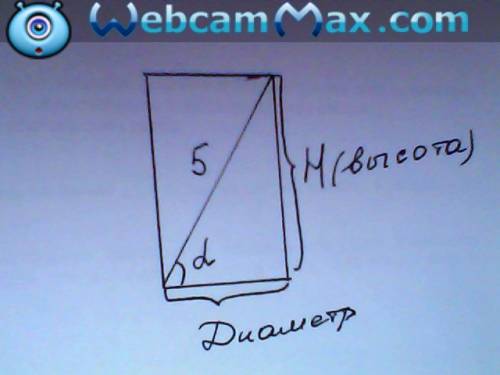
Так как осевое сечение представляет из себя прямоугольник, а диагональ делит его на два прямоугольных треугольника, рассмотрим нижний треугольник:
Так как диагональ, обозначим как D, образует 30 градусов с основанием, тогда имеем высоту цилиндра H равную 2,5.
Диаметр же найдем из прямоугольного треугольника:
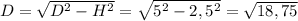
Радиус же будет равен половине диаметра:
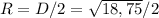
Объем цилиндра равен:
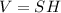, где S-площадь основания H-высота цилиндра
Тогда:
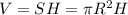
Получаем:
Площадь полной поверхности равна:
Sполной=2Sоснования+Sбоковой поверхности
Имеем:
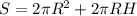
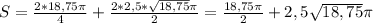
Рисунок рассматриваемого треугольника во вложении
Рabcd = 36 см.
Объяснение:
Треугольники АВС и ADC равны по второму признаку: "Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, такие треугольники равны". В равных треугольниках против равных углов лежат равные стороны, то есть
АВ = AD = 8см и BC = CD = 10см.
Следовательно, периметр четырехугольника АВСD равен
Р = 2(8+10) = 36см.