Объяснение:
Из условия нам известно, что ∠DOC равен пяти углам COB.
Если посмотреть на чертеж, то мы увидим, что ∠DOC и ∠COB смежные, а следовательно, их сумма равна 180°. Для нахождения углов DOC и COB составим линейное уравнение:
Пусть x - ∠DOC, тогда ∠COB - 5x. (угол COB равен 5x, т.к. он в 5 раз больше угла DOC)
Получаем:
x + 5x = 180°
6x = 180°
x = 30° (Это мы нашли x, то есть ∠DOC)
∠COB = 30° * 5 = 150°.
Ну а дальше - дело техники.
∠COD = ∠BOA = 150°(все вертикальные углы равны)
∠BOC = ∠AOD = 30°(все вертикальные углы равны).
Задача решена.
Дано :
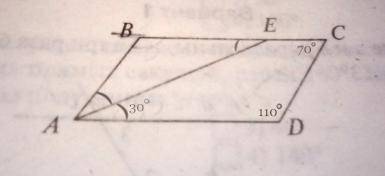
Четырёхугольник ABCD.
Отрезок АЕ - биссектриса ∠BAD.
∠EAD = 30°.
∠C = 70°.
∠D = 110°.
Найти :
∠В = ?
Рассмотрим прямые ВС и AD, которые пересечены секущей CD.
Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то эти прямые параллельны.∠С и ∠D - внутренние односторонние.
∠С + ∠D = 70° + 110° = 180°
Тогда по выше сказанному ВС ║ AD.
Рассмотрим эти же прямые, но тогда, когда они пересечены секущей АЕ.
При пересечении параллельных прямых секущей накрест лежащие углы равны.∠EAD и ∠ВЕА - накрест лежащие.
Тогда по выше сказанному -
∠EAD = ∠ВЕА = 30°.
Рассмотрим ΔАВЕ.
Биссектриса угла треугольника - это отрезок, который делит угол на два равных угла.То есть -
∠ВАЕ = ∠EAD = 30°.
Сумма внутренних углов треугольника равна 180°.Следовательно -
∠ВАЕ + ∠В + ∠EAD = 180°
∠В = 180° - ∠EAD - ∠ВАЕ
∠В = 180° - 30° - 30°
∠В = 120°.
120°.
а КС - 20
то АСК -10 см