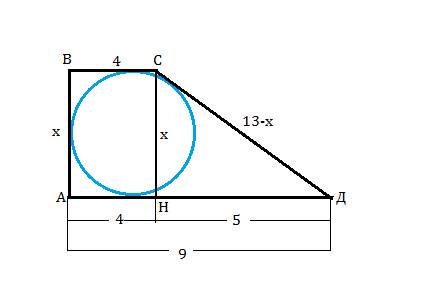
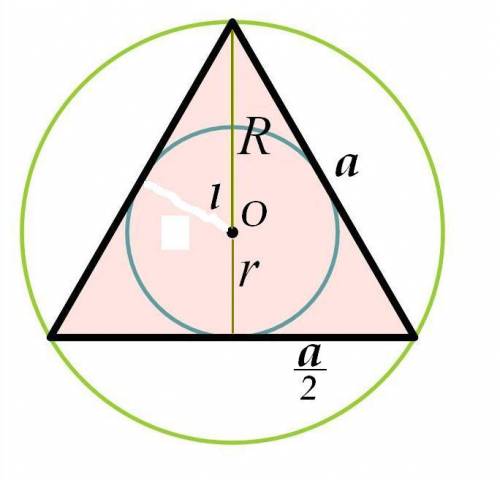
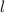 - медиана, биссектриса, высота и серединный перпендикуляр (в равностороннем Δ-ке они совпадают между собой). О - точка пересечения трёх таких линий, как
- медиана, биссектриса, высота и серединный перпендикуляр (в равностороннем Δ-ке они совпадают между собой). О - точка пересечения трёх таких линий, как 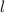 (остальные две на чертеже я не стал чертить). О - центр вписанной и описанной окружностей.
(остальные две на чертеже я не стал чертить). О - центр вписанной и описанной окружностей.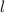 через
через  :
: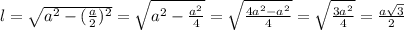
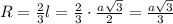
ответ: 1 и 9