Проведём высоту в пирамиде. Проведём перпендикуляры из основания высоты к 4 сторонам, если соединить вершину с точками пересечения, то получаться так же перпендикуляры (по теореме о 3 перпендикулярах), получаются 4 прямоугольных треугольника у которых общий катет и один равный угол (по условию, а так же двугранный угол это линейный угол между 2 перпендикулярами принадлежащих разным плоскостям), то есть эти треугольники равны. Значит в 4 боковых треугольника равны высоты (это гипотенуза от тех прямоугольных треугольников). Так же заметим, что из основания высоты пирамиды проведены 4 перпендикуляры, которые как оказалось равны, то есть это радиусы вписанной окружности в ромбе. Если посмотреть на диаметр этой окружности, то можно заметить, что он перпендикулярен к стороне ромба, то есть радиус это половина высоты от ромба. Высоту в ромбе можно найти перемножив синус угла между смежными сторонами и саму сторону. Далее можно найти радиус ( :2 ). Площадь основания (ромба) можно найти умножим высоту ромба на его сторону. Теперь отвлечёмся от основания и снова посмотрим внутрь пирамиды, там были 4 прямоугольных треугольника, мы теперь знаем его катет, тот что снизу (это радиус вписанной), а так же по условию мы знаем прилежащий к этой стороне острый угол, то есть мы можем найти гипотенузы (поделив катет на косинус угла), как уже было сказано это гипотенуза есть высота в 4 боковых треугольниках пирамиды. У них основание все равны т.к. ромб и высоты тоже все равны, то есть площади все одинаковы. А площадь одного бокового треугольника стоит найти перемножим высоты на сторону и поделив пополам, но у нас же 4 одинаковый площади, так что сразу домножаем на 4 (можно не делить пополам, а сразу умножить на 2). Далее мы складываем площадь основания и боковых ребер. Приведу пример для вычисления площади по моим рассуждениям.
ответ: 54дм
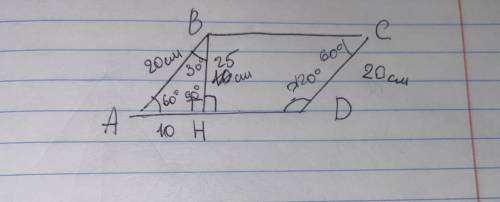
Угол D = 120 градусов.
Объяснение:
1. АВСД - параллелограмм, следовательно:
Ав=сд=20 см , угол а = углу с
2. Вн - высота, следовательно:
Угол ВНА = 90
3. Угол ВНА = 90 градусов, следовательно:
Треугольник ВНА - прямоугольный
4. Рассмотрим ВНА - прямоугольный треугольник:
СD=AB=20 см, АН=10 см
АВ - гипотенуза, АН -катет.
В прямоугольном треугольнике, если катет равен половине гипотенузы, то угол, лежащий против этого катета будет равен 30 градусам. Следовательно угол АВН = 30 градусам, тогда угол А = 180 - угол АВН - угол АНВ= 180 - 30 - 90 = 60
5. Угол А = углу С (по доказанному) = 60 градусам
6. Угол С + Угол Д = 180 градусов (односторонние углы при параллельных прямых в параллелограмме)
Тогда угол Д = 180 - угол С = 120 градусов
Просто