20°
Объяснение:
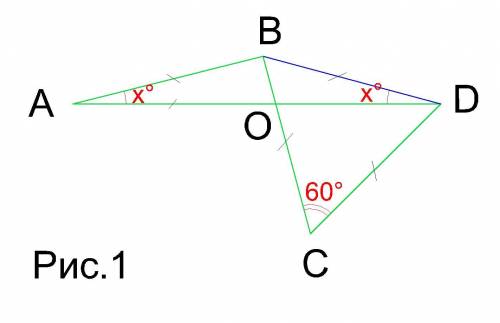
1. Выполним дополнительное построение - проведем отрезок BD.
Получили равносторонний ΔCBD (т.к. ∠С=60° и BC=CD), в котором BC=CD=BD и ∠BCD=∠CBD=∠BDC=60°.
2. Тогда ΔABD - равнобедренный с AB=BD и ∠BAD=∠BDA=x° (см. рис 1)
3. ΔABO - равнобедренный с AB=AO, ∠OAB=x и ∠ABO=∠AOB.
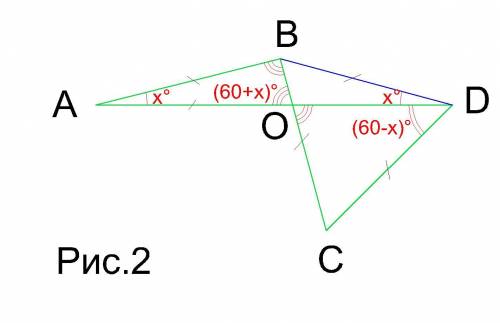
4. Исходя из 1, 2, 3 получаем (см. рис. 2):
∠ODC=(60-x)°
∠COD=180°-60°-(60-x)°=(60+x)°
∠AOB=∠COD=(60+x)° - как накрест лежащие
∠ABO=∠AOB=(60+x)°
Из суммы углов ΔABO:
∠OAB+∠ABO+∠AOB=180° ⇒
x°+(60+x)°+(60+x)°=180°
3x°=60°
x=20°
Угол СHM вписанный,значит он равен половине дуги (СВМ). Следовательно дуга равна 240гр.Вся окружность 360гр.Значит дуга (CHМ) равна 360-240=120гр.Угол СВМ вписанный и равен половине дуги (CHM). Следовательно угол СВМ равен 60гр.
2
Каждая хорда ,проходящая через точку ,лежащую внутри круга,делится в этой точке на отрезки,произведение которых постоянно. Значит РЕ*ЕА=МЕ*ЕК
Пусть РЕ=х,тогда ЕА=х+3
х(х+3)=2*5
х²+3х-10=0
х1+х2=-3 и х1*х2=-10
х1=-5 не удов усл
х2=2
РЕ=2см,ЕА=2+3=5см.Тогда РА=РЕ+ЕА=2+5=7см
ответ РА=7см
3
АВ=20см касательная,ОВ=15см радиус.Соединим точку А с центром окружности.Получили прямоугольный треугольник АВО.Точка С -точка пересечения с окружностью.По теореме Пифагора найдем гипотенузу АО.
АО=√(АВ²+ВО²)=√(400+225)=√625=25см
Тогда расстояние от точки А до окружности рано
АС=АО-СО,СО=ВО=15см
АО=25-15=10см
ответ АО=10см