Цилиндр.
S осевого сечения = 24 (м²).
H (ОО₁) = 3 м.
Найти:S бок поверхности - ? (м²).
Решение:Пусть а - АВ, CD; b - BC, AD.
D - диаметр.
Так как H = OO₁ = 3 м ⇒ AB = CD = H = OO₁ = 3 м.
Осевое сечение этого цилиндра - прямоугольник. Осевое сечение этого цилиндра не может быть квадратом, так как S квадрата = а² = 3² не будет равняться 24 м².
S прямоугольника = ab = 24 (м²).
⇒ b = S прямоугольника/а = 24/3 = 8 (м).
Итак, ВС = AD = 8 (м).
D - BC, AD ⇒ D = BC = AD.
R - радиус.
R = D/2 = 8/2 = 4 (м).
S бок поверхности = 2πRh = π(2 * 4 * 3) = 24π (м²).
ответ: 24π (м²).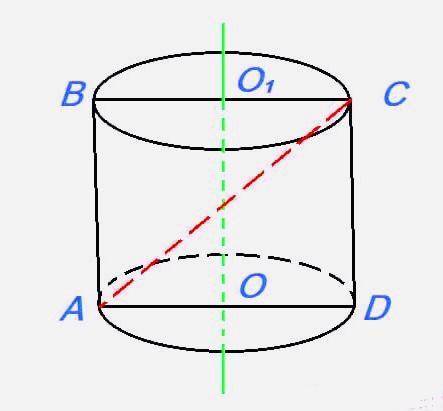
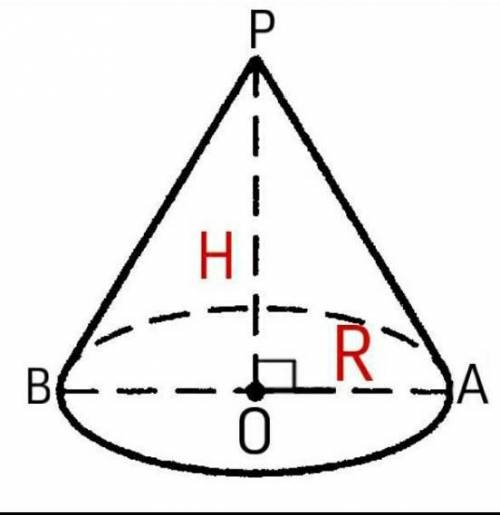
Конус;
R = 12 (м), L = 13 (м).
Найти:S осн - ? (м²).
Решение:Осевое сечение этого конуса (если ось плоскость совпадает с осью конуса) - равнобедренный △ВРА, а высота Н делит этот равнобедренный треугольник на два равных прямоугольных △
△ВРО и △АРО (их равенство можно доказать по всем признакам равенства прямоугольных треугольников, исходя из иого, что △ВРА - равнобедренный).
Найдём высоту Н, по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты).
а = √(c² - b²) = √(13² - 12²) = √(169 - 144) = √25 = 5 (м).
Итак, Н = 5 м
S△BPA = 1/2AB ⋅ H = R ⋅ H = 12 ⋅ 5 = 60 (м²).
ответ: 60 (м²).