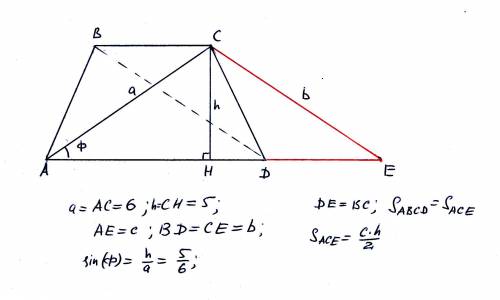
Типовое построение - проводим через вершины малого основания прямую II диагонали, НЕ проходящей через эту вершину, до пересечения с продолжением большого основания. Получается треугольник, РАВНОВЕЛИКИЙ (имеющий ту же площадь) трапеции (у него основание равно сумме оснований трапеции, а высота - общая с трапецией).
В этом треугольнике нам известна одна сторона 6, высота к "основанию" 5, площадь 30, надо найти стороны. Обозначим неизвестные стороны c и b
"основание" находится легко (это с)
с*5/2 = 30, с = 12. (для трапеции это - сумма оснований :))
если обозначить угол между диагональю и основанием Ф, то из этого треугольника находим sin(Ф) = 5/6.
Отсюда сos(Ф) = корень(1 - (5/6)^2) = корень(11)/6;
по теореме косинусов
b^2 = 6^2 + 12^2 - 2*6*12*корень(11)/6 = 180 - 24*корень(11);
b = корень(180 - 24*корень(11));
Так легко же все. Смотрите, АС1 лежит в плоскости АА1С1С (сечение через диагонали верхней и нижней граней и боковые ребра). ВВ1 параллельна этой плоскости. Поэтому расстояние между скрещивающимися прямыми АС1 и ВВ1 равно расстоянию между ВВ1 и плоскостью АА1С1С. Уточняю - где то на ВВ1 есть точка, которая проектируется на плоскость АА1С1С, и проекция попадает на АС1, если быть совсем точным, эта точка находится в центре куба, но это не важно - от любой точки ВВ1 до плоскости АА1С1С расстояние одно и то же. Осталось найти это расстояние. Но оно равно расстоянию от вершины В до диагонали АС квадрата АВСD, то есть
ответ а*корень(2)/2.