Задача на подобие треугольников и теоремы о параллельных плоскостях и прямых.
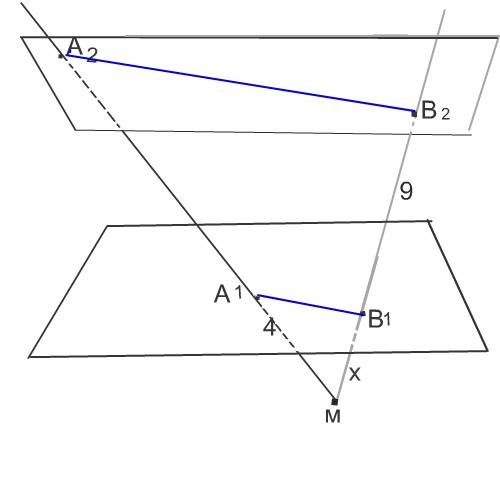
Проведем через точку М, А2 и В2 плоскость.
А1В1 параллельна А2В2 как линии пересечения параллельных плоскостей третьей плоскостью.
Остюда треугольники МА2В2 и МА1В1 подобны.
Примем отрезок МВ1 за х
Тогда МВ2=9+х,
МА2=9+х+4
4:(13+х)=х:(9+х)
36+4х=13х+х²
х²+9х-36=0
При необходимости полное решение квадратного уравнения запишете самостоятельно, а корни его 3 и -12. Второй корень не подходит.
х=3 см
МВ2=9+3=12 см
МА2=12+4=16 см
Задача на подобие треугольников и теоремы о параллельных плоскостях и прямых.
Проведем через точку М, А2 и В2 плоскость.
А1В1 параллельна А2В2 как линии пересечения параллельных плоскостей третьей плоскостью.
Остюда треугольникиМА2В2 и МА1В1подобны.
Примем отрезок МВ1 за х
Тогда МВ2=9+х,
МА2=9+х+4
4:(13+х)=х:(9+х)
36+4х=13х+х²
х²+9х-36=0
При необходимости полное решение квадратного уравнения запишете самостоятельно, а корни его 3 и -12. Второй корень не подходит.
х=3 см
МВ2=9+3=12 см
МА2=12+4=16 см
Вектор СВ: ((-1)-2)=-3; 5-0=5) = (-3;5).
Вектор ДА: (3-(-3)=6; 2-(-4))=6) =(6;6).
Формула вычисления угла между векторами:cos α = (a·b)/|a|·|b|.
Найдем скалярное произведение векторов:
a·b = -3*6 + 5*6 = -18 + 30 = 12.Найдем модули векторов:
|a| = √((-3)² + 5²) = √(9 + 25) = √34,|b| = √(6²+6²) = √(36 + 36) = √72 = 6√2.
cos α = (a*b)/(|a|*|b|) = √34/√72 = 0,687184.
Угол равен arc cos(0,687184) = 0,81319 радиан = 46,59237 °.