Объяснение:
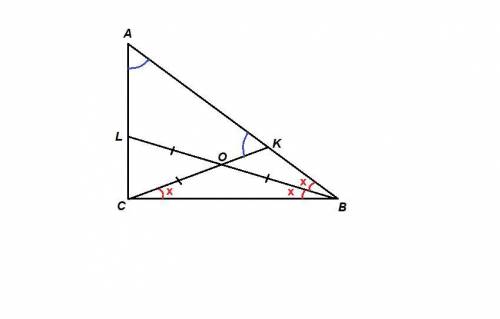
ΔLBC: ∠LCB = 90°, О - середина гипотенузы LВ, ⇒ СО - медиана, проведенная к гипотенузе, равна половине гипотенузы. Значит
ВО = OL = ОС.
Пусть половине угла В - х.
∠ОСВ = ∠ОВС = х, как углы при основании равнобедренного треугольника ОВС.
Тогда ∠АСК = 90° - х.
ΔАСК равнобедренный, так как СК = АС по условию, значит
∠САК = ∠СКА = (180° - ∠АСК) / 2 =
= (180° - (90° - x)) / 2 = (180° - 90° + x) / 2 = (90° + x) / 2
Сумма острых углов прямоугольного треугольника равна 90°:
∠САК + ∠АВС = 90°
Получаем уравнение:
(90° + x) / 2 + 2x = 90° | ·2
90° + x + 4x = 180°
5x = 90°
x = 18°
∠ABC = 2 · 18° = 36°
3) 50 градусов.
Объяснение:
3) Внутренний угол В равен: 180-110=70 градусов, так как углы смежные.
Внутренний угол С равен: 180-120=60 градусов, так как углы смежные.
Так как сумма углов в треугольнике равна 180, то внутренний угол А равен: 180-70-60=50 градусов.
ответ: 50 градусов.
4) Треугольники ADB и DCB равны по стороне и двум прилежащим к ней углам (DB общая, угол 1 равен углу 2 по условию, угол 3 равен углу 4 по условию).
Так как треугольники равны, то стороны AB и CB равны, стороны AD и DC равны, значит, треугольники АВС и ADC равнобедренные.
В равнобедренных треугольниках биссектриса, проведенная к основанию, является также и высотой, значит DO перпендикулярна AC, ВО перпендикулярна АС.
DB перпендикулярна AC.
Утверждение доказано.