Для начала нарисуем произвольную трапецию АВСD и через точку Е проведем прямую EF параллельную основаниям трапеции
Найдем площадь треугольника CEF, которая равна EF*h1/2, затем найдем площадь треугольника DEF, которая также равна EF*h1/2.
Площадь треугольника ЕСD равна сумме площадей этих треугольников
EF*h1/2 + EF*h1/2 = EF*h1
EF - средняя линия трапеции и равна она половине суммы оснований, а именно (а+в)/2;
высота h1 равна половине высоты трапеции, а именно h/2.
Осталось только подставить значения
EF*h1 = (а+в)/2*h/2 = (а+в)*h/4 и сравнить
площадь трапеции формула
Площадь треугольника ЕСD равна половине площади трапеции, что и требовалось доказать.
Сделаем рисунок.
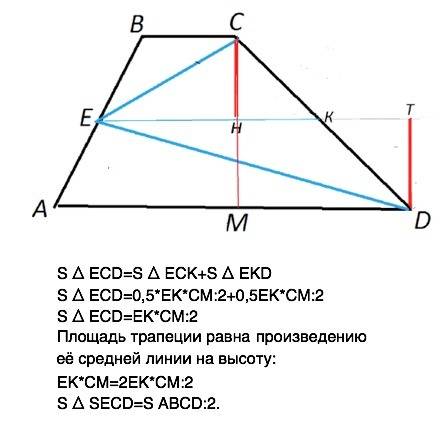
От середины АВ проведем ЕК - среднюю линию трапеции.
ЕК делит треугольник ЕСD на два: ᐃ ЕСК и ᐃ ЕКD.
ЕК по свойству средней линии делит высоту СМ трапеции пополам,
и СН=МН=DТ=0,5*СМ (см. рисунок)
Треугольники ЕСК и ЕКD равновелики: площадь каждого равна
половине произведения их общего основания ЕК, являющегося
средней линией трапеции АВСD, на половину её высоты.
S ᐃ ECD=S ᐃ ECK+S ᐃ EKD
S ᐃ ECD=0,5*EK*CM:2+0,5EK*CM:2
S ᐃ ECD=EK*CM:2
Площадь трапеции равна произведению её средней линии на высоту.
ЕК*СМ=2EK*CM:2
S ᐃ SECD=S ABCD:2, что и требовалось доказать.
если диагональ квадрата уменьшить два раза то его площадь тоже уменьшится в 2 раза.