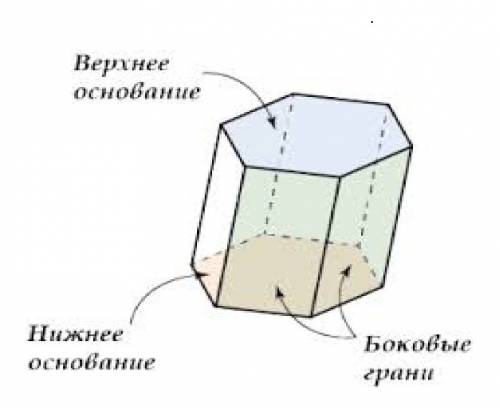
Количество всех ребер призмы равно сумме боковых ребер и ребер двух оснований.
Пусть количество сторон (ребер ) каждого основания призмы n, значит, и вершин у одного основания n
Боковых ребер будет тоже n, т.к. они соединяют вершины верхнего и нижнего основания, т.е. их столько, сколько вершин в одном основании.
Тогда всех ребер 2n+n=3n
3n=36
n=12. Это значит, что у каждого основания призмы 12 сторон (ребер).
Следовательно. боковых граней тоже 12.
А всего 12 боковых +2 основания=14 граней.
------
Для примера можно рассмотреть простую призму - куб.
Сторон (ребер) одного основания -4, боковых ребер -4, всего - 12 ребер
Боковых граней - 4, всего 4+2=6.
В параллелограмме abcd биссектриса угла a пересекает сторону bc в точке p ,bp:pc=4:3. периметр параллелограмма равен 110 см. найдите стороны параллелограмма
Объяснение:
Дано:
АВСD-параллелограмм ,
АР-биссектриса,
ВР/РС=4/3 , Р=110 см
Найти:
АВ, ВС, АС, СD.
Решение.
АР- биссектриса, значит ∠ВАР=∠РАD.Пусть одна часть х, тогда ВР=4х, ВС(4+3)*х=7х. По свойству противоположных сторон АD=7х.
Т.к. АD║ВС , АP-секущая , то накрест лежащие углы равны ∠DAP=∠ВКP ⇒ΔАВК-равнобедренный по признаку равнобедренного треугольника ⇒АВ=ВP=4х.
Р=АВ+ВС+СD+СD
4х+7х+4х+7х=110,
22х=110 , х=5 .
АВ=СD=4*5=20 (см),
ВС=СD=7*5=35 (см).