41) ∠4 = 145°
43) ∠1 = 40
49) ∠AKD = 10°
Объяснение:
41) Поскольку ∠3 + ∠1 = 180 и ∠3 - ∠1 = 110 составим систему уравнений (пусть ∠3 = х, ∠1 = y ):
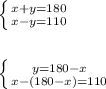
Решим вторую часть системы.
x - (180 - x) = 110
2x = 110 +180
2x = 290
x = 145
∠3 = 145°, следовательно ∠4 тоже будет равен 145°, так как это вертикальные углы.
43) ∠3 = 180° - ∠ACD(∠1+∠2) = 180 - 110 = 70° (так как смежные)
Поскольку CD - биссектриса ∠ECB, следовательно ∠3 = ∠2 = 70°
∠1 = 180 - ∠ECB (∠2+∠3) = 180 - 140 = 40° (опять-таки так как эти углы смежные)
49) Так как KE - биссектриса ∠CKB, тогда ∠EKB = ∠CKE = 40°
Так как DK ⊥CK, значит ∠ DKC = 90°
∠DKB = ∠EKB + ∠CKE + ∠DKC = 40 + 40 + 90 = 170°
∠AKD = 180° - ∠DKB = 180- 170 = 10° (так как ∠AKD и ∠DKB смежные)
АВ - первая сосна,
CD - вторая сосна,
AD - расстояние между ними.
Если считать, что сосны растут перпендикулярно земле, получаем прямоугольную трапецию с основаниями АВ и CD, в которой большая боковая сторона ВС - искомая величина.
Проведем СН - высоту трапеции.
СН = АD = 20 м, как расстояния между параллельными прямыми,
СН║AD как перпендикуляры к одной прямой, значит AHCD - прямоугольник, ⇒
АН = CD = 12 м
ВН = АВ - АН = 27 - 12 = 15 м
Из прямоугольного треугольника ВСН по теореме Пифагора:
ВС² = ВН² + НС² = 15² + 20² = 225 + 400 = 625
ВС = 25 м