а) радіус R кола, описаного навколо основи піраміди.
Радиус R равен половине диагонали квадрата основания.
Проекция апофемы на основание равна 4 см, так как равна высоте пирамиды.
Тогда половина диагонали равна 4√2 см и равна R.
ответ: R = 4√2 см.
б) радіус r кола, вписаного в основу піраміди.
Радиус r равен половине стороны основания и равен проекции апофемы на основание (найдена выше).
ответ: радиус r равен 4 см.
в) площу основи піраміди.
Сторона основания а = 2r = 2*4 = 8 см.
ответ: S = a² = 8² = 64 см².
ответ: V=a³•sin²α•tgβ/6
Объяснение - очень подробно:
Формула объема пирамиды V=S•h/3, где S – площадь основания пирамиды, h - её высота.
Стороны ромба равны. По условию боковые грани наклонены к плоскости основания под углом β.
Если боковые грани пирамиды наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проецируется в центр этой окружности.
Центр окружности, вписанной в ромб – точка пересечения его диагоналей, а расстояние от него до сторон равно радиусу вписанной окружности.
Высота пирамиды, радиус вписанной окружности и высота боковой грани образуют прямоугольный треугольник, при этом высота боковой грани и радиус вписанной окружности образуют линейный угол между основанием и боковой гранью, т.к. по т. о 3-х перпендикулярах перпендикулярны стороне ромба (ребру двугранного угла) в одной точке.
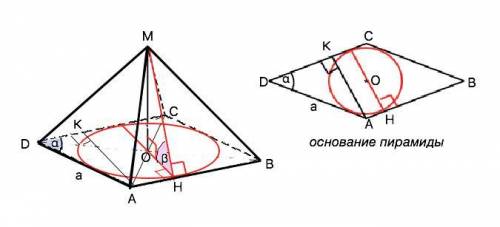
Диаметр окружности, вписанной в ромб, перпендикулярен его сторонам, параллелен высоте ромба и равен ей. На рисунке приложения АК = высота ромба. АК=АD•sinα=a•sinα ⇒ HO=r=a•sinα•1/2. Из прямоугольного ∆ МОН высота пирамиды МО=ОН•tgβ=(a•sinα•1/2)tgβ
S(ABCD)=AD•CD•sinα=a²•sinα
V=a²•sinα•(a•sinα•1/2)tgβ/3=a³•sin²α•tgβ/6
Дано: треуг. АВС - равнобедренный(р/б) с основание АВ ;
СН - высота, М - лежит на СН.
Д-ть: треун.АМB - р/б.
Док-во:
в р/б треугольнике высота , проведённая к основанию , делит его пополам (наш случай:) ; Значит, АМ=АВ => треуг.АМВ - равнобедренный , ч.т.д.