Задачі на кути трикутника з розв'язками
Задачі на кути трикутника не важкі, якщо мова йде про 8, 9 клас школи. Але коли йде мова про медіани, бісектриси чи певні побудови то знаходження кутів в трикутнику не таке просте, як може здатися з умов. Далі наведені завдання складнішого типу, вони цікавіші, а їх аналіз точно Вас чогось навчить.
Приклад 30.26 Бісектриса гострого кута прямокутного трикутника утворює з протилежною стороною кути, один з яких дорівнює 70 градусів.
Знайти у градусах менший гострий кут трикутника.
Розв'язування: Нехай маємо прямокутний трикутник ABC (∠C=90), AL – бісектриса, яка проведена до сторони BC, тоді ∠ALC=70 градусів (за умовою).
Побудуємо рисунок трикутника та бісектриси в ньому
ответ: 600 см²
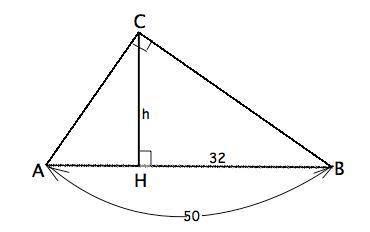
Объяснение: Проекции катетов - это отрезки гипотенузы, на которые делит ее высота, проведенная к ней из прямого угла.
Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу.
Обозначим гипотенузу АВ, высоту из прямого угла – СН. ⇒
СН=√(АН·ВН)
СН=√(50-32)·32 =√576=24
Площадь треугольника равна половине произведения высоты на сторону, которую она пересекает. ⇒
Ѕ(АВС)=24·50·0,5=600 см²
1.
Дано: КМРТ - параллелограмм, МР=16 см, КМ=13 см, ∠М=150°. Найти S(КМРТ).
Проведем высоту МН. Рассмотрим ΔКМН - прямоугольный. ∠КМН=150-90=60°, ∠МКН=90-60=30°.
МН=1/2 КМ=13:2=6,5 см по свойству катета, лежащего против угла 30 градусов.
S=16 * 6,5=104 см²
см²)
2.
Дано: КМРТ - параллелограмм, КТ=21 см, РТ=10 см, МВ - высота, МВ=12 см. Найти высоту МН.
Найдем высоту через площадь параллелограмма.
S=РТ*МВ=10*12=120 см², тогда
120=КТ*МН; 21*МН=120; МН=120/21=40/7=5 5/7 см.