АС - більша діагональ, ВД - менша.
АС - ВД = 10см
Нехай ВД = х см, АС = 10 + х см
Діагоналі перетинаються під прямим кутом і діляться навпіл.
СО = ОА = (10 + х) / 2
ВО = ОД = х/2
Розглянемо трикутника ВСО:
він прямокутний кут О = 90градусів
Застосуємо теорему Піфагора:
ВС² = ВО² + СО²
25² = ((10 + х)/2)² + (х/2)²
625 = (100 + 20х + х²)/4 + х²/4
625 = (100 + 20х + 2х²) / 4
625 = (2 * (х² + 10х + 50)) / 4
625 = (х² + 10х + 50) / 2
1250 = х² + 10х + 50
х² + 10х - 1200 =0
шукай по дискрімінанту
Д = 70²
х1 = 30, х2 = -40
х2 = -40 -незадовільняє умову (довжина не може бути відємною)
Отже ВД = 30 см, АС = 30 + 10 = 40 см
S = 1/2 * АС * ВД = 1/2 * 30 * 40 = 600 см²
700/28*5=125
Объяснение:
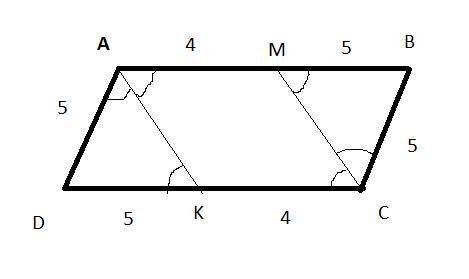
Обозначим параллелограмм ABCD так, что углы A и C - тупые. Проведем биссектрисы AK, и CM. Т.к. ABCD - параллелограмм, то углы DAB и BCD равны, и соответственно т.к. AK и CM биссектрисы, то углы
<DAK=<KFB=1/2 <DAB (здесь и далее "<" - значёк угла)
<BCM=<MCD=1/2 < BCD, и значит
<DAK=<KFB=<BCM=<MCD
углы <BAK и <AKD - накрестлежащие, следовательно <BAK = <AKD
углы <KCM и <BMC - накрестлежащие, следовательно <KCM = <BMC
в итоге <AKD=<DAK, <BMC=<BCM, треугольники KDA и MBC - равнобедренные, отсюда AD=DK и BM=BC.
Вводим условные единицы длины, с учетом того, что биссекутрисса делит противоположную сторону в соотношениие 4:5 так, что BM=5уе, AM=4уе, далее очевидно периметр параллелограмма равен 28 уе, 1уе=700/28=25
Очевидно из рисунка - меньшая сторона параллелограмма равна 5уе=5*25=125
cosA = (10² + 12² - 8²)/(2•10•12) = 180/ 240 = 0,75
По таблице находим угол
arccosA ≈ 41°24'.