Углы, образованные при пересечении двух параллельных прямых секущей, или равны, или в сумме составляют 180°. Следовательно, нам дано значение одного из смежных углов.
а) второй угол равен 180° - 150° =30°.
б) один из углов равен Х градусов, второй - Х+70 градусов. Их сумма равна 2Х+70=180° => X=55°. Тогда меньший угол = 55°, второй = 125°.
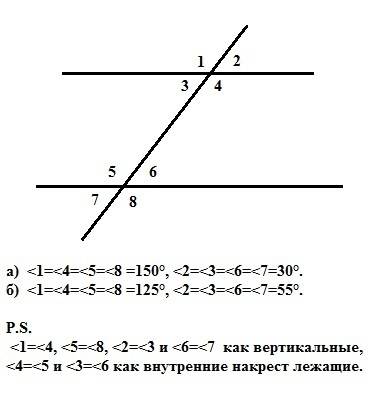
Или (см. рисунок): а) <1=<4=<5=<8 =150°, <2=<3=<6=<7=30°.
б) <1=<4=<5=<8 =125°, <2=<3=<6=<7=55°.
P.S.
<1=<4, <5=<8, <2=<3 и <6=<7 как вертикальные,
<4=<5 и <3=<6 как внутренние накрест лежащие.
Соединив точки А и Р, получим прямоугольную трапецию АРСД.
Диаметр вписанной в трапецию окружности равен ее высоте, здесь - стороне АВ=СД, т.е. 4. Радиус r=2 см
Проведем из центра О радиусы в точки касания окружности с ВС и СД. Отрезки касательных, проведенные из одной точки, равны.
КС=СЕ=r=2 см.
ВК=ВС-КС=5-2=3 см
Обозначим М середину АВ, Е - середину СД.
МО=ВК=3 см
АМ=СЕ=ДЕ=4:2=2 см
По т.Пифагора или как гипотенуза равнобедренного ∆ ОЕД –
ОД=2√2.
Р (АМОД)=АД+АМ+МО+ОД=5+2+3+2√2=(10+2√2) см или ≈ 12, 828 см