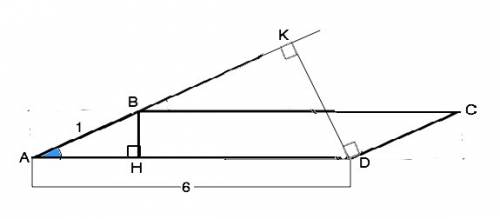
Одна из формул площади параллелограмма Ѕ=a•h. Очевидно, что при одинаковой площади большей будет высота, проведенная к меньшей стороне, и наоборот. Следовательно, искомой будет высота к стороне АВ ( или равной ей CD).
На рисунке в приложении высота к меньшей стороне АВ пересекается с ее продолжением. Из прямоугольного треугольника AKD высота DK=AD•sinA=6•1/3=2 (ед. длины)
Как вариант можно найти большую высоту иначе. Сначала найти длину меньшей высоты ВН=АВ•sinA, затем найти площадь S=ВН•AD и высоту DK=S:AB.
Рассмотрим ∆ АВD и ∆ СВЕ
Оба прямоугольные и имеют общий острые угол АВС.
Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.
Из подобия следует отношение
ВЕ:ВD=ВС:АВ⇒ВD•ВС=ВЕ•АВ ⇒
ВЕ:ВС=ВD:АВ
Две стороны ∆ ВЕD пропорциональны двум сторонам треугольника АВС, и угол между ними общий.
2-й признак подобия треугольников:
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
Следовательно, ∆АВС и ∆ ВЕD подобны, что и требовалось доказать.
Можно добавить. что коэффициент подобия равен косинусу общего угла, т.к. отношение катетов ∆ СВЕ и ∆ АВД к их гипотенузам соответственно равны косинусу угла В треугольника АВС.

1) угол АОВ = 180 - 60 =120 градусов
2) Проведём биссектрису СК. Она пройджёт через точку О и будет одновременно медианой
то есть АК =6/2=3см и высотой, то есть угол АКО =90 градусов и угол АОК = 120/2 =60 градусов
3) Из тр-ка АКО имеем АО = АК/ sin60 = 3 : ( √3/2) = 2√3
4) По свойству медиан АА1 = 1,5АО =1,5 *2√3 =3√3
ответ АА1 =3√3
2)пусть одна сторона-х, тогда другая- 13-х, по теореме косинусов сост. уравнение:
x^2+(13-x)^2-2*x*(13-x)*cos60=49
x^2+169-26x+x^2-13x+x^2=49
3x^2-39x+120=0
x^2-13x+40=0
D=169-160=9 x1=(13+3)\2=8 x2=(13-3)\2=5
х=8-одна боковая сторона, 13-8=5-другая или наоборот х=5, 13-5=8.