a = 5 см,
b = 4 см,
c = 7 см.
Найти R.
Запишем теорему синусов:
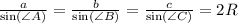
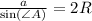
числитель и знаменатель дроби слева последнего равенства домножим на (b·c).
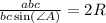
С учётом того, что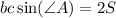 
, где S - площадь данного в условии треугольника, имеем
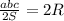
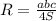
Площадь треугольника можно найти по формуле Герона:
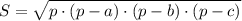, где
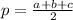
Найдем, сначала, площадь треугольника.
p = (5+4+7)/2 = (9+7)/2 = 16/2 = 8 см.
S = √(8·(8-5)·(8-4)·(8-7)) = √(8·3·4·1) = 4·(√6) см²
Теперь найдем радиус описанной окружности.
R = 5·4·7/(4·4·(√6)) = 5·7/(4·(√6)) = 35·(√6)/(4·6) = 35·(√6)/24 см.
Теперь найдём длину окружности, описанной около данного треугольника.
L = 2πR = 2π·35·(√6)/24 см = π·35·(√6)/12 см.
Люди никогда не всматриваются в то, что нас окружает, а если присмотреться то можно найти множество интересных конструкций, геометрических фигур, а так же и параллельных прямых. Параллельными могут быть этажи в доме, левый и правый край бордюра, противоположные стороны у двери и многое другое. Возможно люди не засматриваются на это, потому что им это не интересно или не надо. Ну посудите сами если засматриваться на параллельные прямые, то мы будем терять время попросту, на то что нам не пригодиться. Но вот некоторым людям это надо, к примеру строителям. Если они не правильно будут класть камни, т.е. не параллельно, то конструкция сломается, а это не хорошо. Так что параллельных прямых много вокруг нас, мы просто их не замечаем.
