
Объяснение:
координаты вектора вычисляются так: из соответствующей координаты конца вектора нужно вычесть соответствующую координату начала вектора.
получим координаты вершин параллелограмма, выраженные через координаты одной точки (точки А, например)
координаты векторов-диагоналей параллелограмма вычисляются аналогично...
косинус угла между векторами = частному от деления скалярного произведения векторов на произведение длин векторов.
скалярное произведение векторов=сумме произведений соответствующих координат.
длина вектора=корню квадратному из суммы квадратов координат (т.Пифагора)
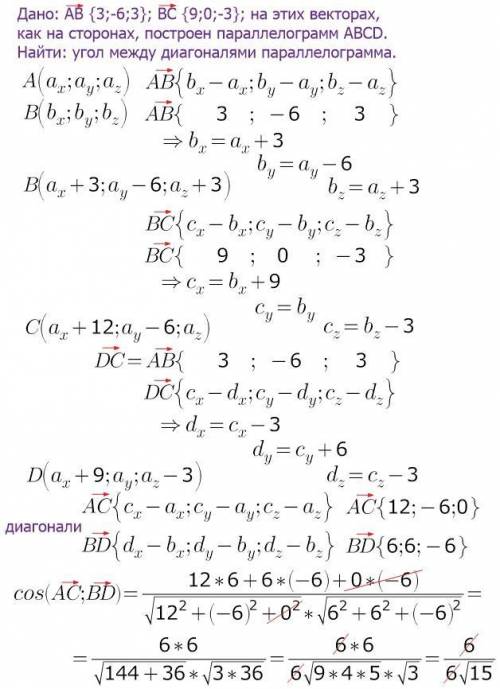
2х+3х=180
5х=180
х=180/5
х=36
2х=36*2=72
3х=36*3=108
угол 5 равен углу 4 как накрест лежащие
угол 5 равен углу 1 как соответственные
угол 4 равен углу 8 как соответственные
угол 3 равен углу 7 как соответственные
угол 3 равен углу 6 как накрест лежащие
угол 6 равен углу 2 как соответственные