Объяснение:
SA₁B₁C₁=S
Медианы делят треугольник на 6 равновеликих треугольников с площадями SABC/6
тогда площади треугольников SOAB=SOAC=SOBC=(1/3)SABC так как каждый из них состоит из двух таких треугольников
и медианы в точке пересечения делятся в отношении 1:2
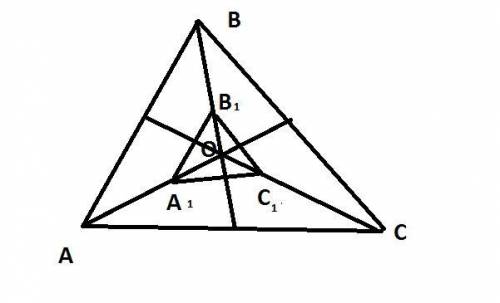
пусть точка О- точка пересечения медиан
тогда получается что
OA=(2/3)AA₂
AA₁=(1/2)AA₂
OA₁=(2/3)AA₂-(1/2)AA₂=(1/6)AA₂
OA₁/OA=(1/6)AA₂/(2/3)AA₂=1/4
аналогичным образом
OB₁/OB=1/4
OC₁/OC=1/4
тогда треугольники OA₁B₁, OA₁C₁, OB₁C₁ подобны треугольникам OAB, OAC, OBC с коэффициентом подобия 1/4
отношения площадей подобных фигур равно квадрату коэффициента подобия то есть (1/4)²=1/16
SOA₁B₁=(1/16)SOAB
SOA₁C₁=(1/16)SOAC
SOB₁C₁=(1/16)SOBC
сложим эти равенства
SOA₁B₁+SOA₁C₁+SOB₁C₁=(1/16)(SOAB+SOAC+SOBC)
SA₁B₁C₁=(1/16)SABC
SABC=16SA₁B₁C₁=16S
SABC=16S
6 ед.
Объяснение:
В правильной усеченной пирамиде в основаниях лежат правильные многоугольники, стороны которых соответственно равны между собой. Боковые грани такой пирамиды - равные между собой равнобокие трапеции. Радиусы окружностей, вписанных в основания, проведенные в точки касания сторон оснований с соответственной окружностью Н и Н1, перпендикулярны к сторонам оснований по свойству радиусов, проведенных в точки касания.
Проведем перпендикуляр из точки касания Н1М верхнего основания на нижнее основание. Тогда отрезок Н1Н перпендикулярен стороне основания АВ по теореме о трех перпендикулярах, то есть является искомой высотой боковой грани.
В прямоугольном треугольнике НН1М угол ∠НН1М = 30° по сумме острых углов. Следовательно, НН1 = 2·НМ по свойству катета, лежащего против угла 30°.
НМ = ОН - О1Н1 = 8-5 = 3 ед.
Высота боковой грани НН1 = 6 ед.