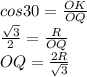
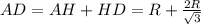
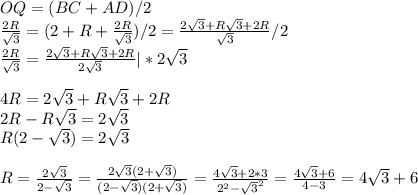
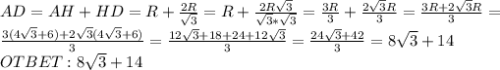
Основания - правильные треугольники. О₁ - центр верхнего основания (точка пересечения медиан (биссектрис, высот)), О - центр нижнего основания.
Пусть Н - середина В₁С₁, тогда О₁Н - радиус окружности, вписанной в треугольник А₁В₁С₁.
О₁Н = а√3/6 = 6√3/6 = √3 см
Пусть К - середина ВС, тогда ОК - радиус окружности, вписанной в треугольник АВС:
ОК = 12√3/6 = 2√3 см.
ОО₁ - высота пирамиды, тогда
ОО₁⊥ВС и АК⊥ВС, т.е. ребро ВС перпендикулярно двум пересекающимся прямым плоскости АКН, значит
ВС⊥(АКН)
Тогда ВС⊥КН, ∠НКА = 30° и НК - апофема пирамиды.
Sбок = (P₁ + P₂) · HK, где P₁ и P₂ - периметры оснований.
Осталось найти НК.
ОО₁НК - прямоугольная трапеция. Проведем в ней высоту НТ.
ОО₁НТ - прямоугольник, ОТ = О₁Н = √3 см
ТК = ОК - ОТ = 2√3 - √3 = √3 см
ΔНТК: cos 30° = TK / HK
HK = TK / cos 30° = √3 / (√3/2) = 2 см
Sбок = (P₁ + P₂) · HK = (6 ·3 + 12 · 3) · 2 = (18 + 36) · 2 = 54 · 2 = 108 см²
Точка Е - середина КР⇒ КЕ=РЕ.
МЕ входит в периметры как ∆ МКЕ, так и ∆ МЕР, 13 см, поэтому на самом деле 13 см - это разность между (МК+КЕ) и (МР+РЕ).
Вариант а) МР< МК+КЕ
Пусть КЕ=ЕР=а. Тогда МК=2а
(2а+а)-(22+а)=13⇒ 2а-22=13⇒2а=35 см
МР=МК=35 см
---------
Вариант б) МР+ЕР > МК+ЕК
22+а-3а=13⇒2а=9 см
2а=9. В этом варианте не соблюдается неравенство треугольника, где наибольшая сторона треугольника не может быть больше суммы двух других сторон или быть равна ей.
Следовательно, боковые стороны этого треугольника равны 35 см