Как из площади вписанного в окружность правильного шестиугольника найти радиус? ?

👇

Ответ:

вероника1060

17.12.2022

Надеюсь то.

Сторона правильного шестиугольника равна радиусу Описанной около него окружности. Соединим концы стороны шестиугольника с центром окружности. Получим правильный треугольник. Площадь правильного треугольника равна S=(√3/4)*R². Таких треугольников 6.
В нашем случае S=6√3дм².
Или:
Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне. Высота правильного треугольника по Пифагору равна √(а²-а²/4)=а√3/2.
Тогда его площадь равна S=(1/2)*a*a√3/2 или S=a²√3/4. Вот мы и вывели формулу. далее, как уже было сказано: площадь шести таких треугольников равна а²√3*3/2. а=2дм. S=6√3дм²
ответ: S=6√3 дм²

4,8(100 оценок)

Открыть все ответы

Ответ:

sashapeterov85

17.12.2022

4.
V = a³ куба
a = ∛V сторона куба
a = ∛36
R = a/2 = ∛36/2 радиус шара
V = 4/3πR³ шара
V = 4/3 * π * (∛36/2)³ = 4/3 * π * 36/8 = 6π
V = 6π = 6 * 3 ≈ 18

3.
S = πR² основания
R = √(S/π) радиус
R = √(49π/π) = √49 = 7
R = 7
D = 2R = 14 диаметр
В осевом сечении треугольник , где D - основание, h - высота
S Δ = 1/2 * D * h
h = 2S/D
h = 2 * 42 : 14 = 6
h = 6
V = 1/3 * S * h
V = 1/3 * 49π * 6 = 98π
V = 98π ≈ 98 * 3 ≈ 294
1.
В осевом сечении прямоугольник, где (d) диаметр и (h) высота - его стороны
d = 2R , значит,
d - 2 части
h - 2 части
Вывод: это квадрат с диагональю 8√2
По теореме Пифагора
x² + x² = (8√2)²
2x² = 64 * 2
x² = 64
x = √64 = 8 - это диаметр , высота такая же h = 8
R = 8/2 = 4
V = π * R² * h
V = π * 4² * 8 = 3 * 16 * 8 ≈ 384
V ≈ 384

2.
V = 1/3 * S * h
S = (10√3 )² = 100*3= 300
Из прямоугольного треугольника, образованного высотой пирамиды, апофемой и полустороной a/2, находим высоту h
h = a/2 * tg 60°
h = 8√2/2 * √3 = 4 * √6
h = 4√6
V = 1/3 * 300 * 4√6 = 400√6 ≈ 980

4,5(55 оценок)

Ответ:

helppliizzzz

17.12.2022

ответ: 432π

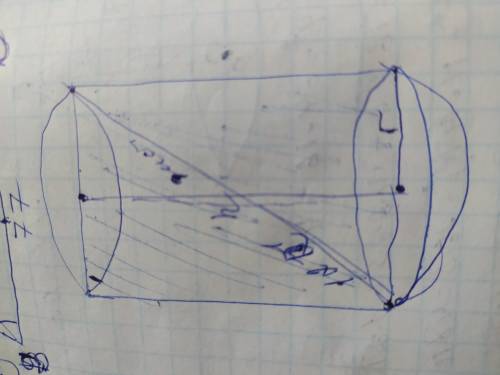
Объяснение: обозначим радиус r, a высоту h. Если r/h=1/2, то: h=2r. 2 радиуса

- это диаметр, и диаметр основания равен высоте. Высота, радиус и диагональ осевого сечения цилиндра образуют равнобедренный прямоугольный треугольник, в котором диаметр основания и высота являются катетами а диагональ гипотенузой. В равнобедренном прямоугольном треугольнике гипотенуза больше катета в √2 раз, поэтому h=диаметру=12√2/√2=

=12, тогда радиус=12/2=6

Найдём площадь основания по формуле:

Sосн=πr²=π×6²=36π

Теперь найдём объем цилиндра зная его площадь основания и высоту по формуле: V=Sосн×h=36π×12=432π(ед³)