Меньшее основание равно 11 см
Объяснение:
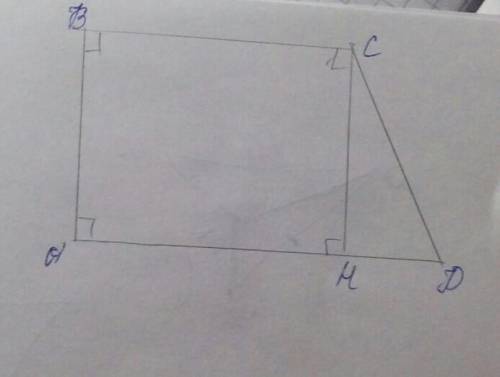
Сделаем дополнительное построение высоту CH проведенную из угла C.
Если в треугольнике HCD угол D равен 45 градусам, то угол HCD = 45 градусам, так как треугольник HCD прямоугольный : 180-(уголCHD+угол CDH)= 180-(45+90)= 45, а значит треугольник HCD равнобедренный (по признаку), а значит сторона CH равна стороне HD CH=HD=20см.
AD-HD=AH=11см(по св-ву измерения отрезков) а так как abch - прямоугольник( угол b=90, угол а =90, угол bch=90, cha=90) (по определению прямоугольника), AH=BC=11см( по св-ву прямоугольника)
V=96*pi (см.куб.)
Объяснение:
Дано:
S_бок.пов.=48*pi (см.кв.)
l=r+2, где l- образующая цилиндра, r -его радиус.
V-?
В цилиндре все образующие параллельны его оси и равны его высоте, т.е.
l=h. (1)
По определению
S_бок.пов.=2*pi*r*h, (2)
V=pi*(r^2)*h. (3)
С учетом (1) для (3) имеем
V=pi*(r^2)*l. (3а)
Подставим в (2), с учетом (1), данные из условия задачи и упростим полученное выражение:
S_бок.пов.=2*pi*r*l--->48*pi=2*pi*r*l--->24=r*l.
Отсюда l=24/r. С другой стороны, по условию l=r+2. Поэтому можно записать:
r+2=24/r.
Данное выражение можно переписать в форме:
r^2+2*r-24=0. (4)
Решая уравнение (4), находим его корни r_1=4 и r_2=-6. Так как, радиус - положительно определённая величина, то r_2 не может являться радиусом цилиндра. Следовательно, r=4 см. Далее, получаем l=r+2=4+2=6см.
Таким образом, подставляя числовые значения r и l в формулу (3a), получаем
V=pi*(4^2)*6=pi*16*6=96*pi (см.куб.)
x' = x-2;
y' = y+3;
Выразим из последних уравнений икс и игрек, то есть выразим старые координаты через новые:
x = x' +2;
y = y' - 3;
и подставим это в исходное уравнение:
(x'+2) + 2*(y'-3) - 2 = 0;
x'+2 + 2y' - 6 - 2 = 0;
x' + 2y' - 6 = 0.
Последнее уравнение и есть искомое.