ответ:7) АСД=90° и АСВ=90° 13) АСВ=30° 11) ∠2=30° и ∠ 1=90°
Объяснение:7) В ΔАДС М- центр описанной окружности ⇒ АД= диаметр этой окружности и Δ АДС- прямоугольный,т.к. ∠АСД-вписанный и опирается на диаметр ⇒ ∠АСД=90°.
ДС- наклонная к пл. АВС, ДС ⊥ АС, АС⊂пл.АВС,ВС-проекция ДС на пл. АВС. По теореме о 3-х перпендикулярах ВС⊥АС ⇒ ∠ АСВ=90° ответ: 90° и 90°
13) АД, СД и ВД-наклонные к пл.АВС, АД=СД=ВД по условию.
АО,ВО и СО - проекции этих наклонных на пл. АВС ⇒ АО=ВО=СО
О-центр описанной окружности около ΔАВС. ∠АОВ=60° и является центральным углом ⇒ ∪АВ =60°; ∠ АСВ -вписанный угол, опирающийся на ∪АВ ⇒ ∠АСВ=30° по свойству вписанного угла. ответ: 30°
11) В условии задачи есть опечатка: АД=2ВД вместо АМ=2ВД.
В ΔАВД ВД⊥пл.АВС и АВ⊂пл.АВС ⇒∠ДВА=90°, АД=2ВД⇒ ∠ДАВ= ∠2= 30° по свойству катета напротив угла 30° .
ДС-наклонная к пл.АВС, АС ⊂ пл.АВС и ∠АСД=90° по условию, ВС- проекция ДС на пл.АВС . По теореме о 3-х перпендикулярах ДС ⊥АС
и ∠ДСА= ∠ 1=90°. ответ: ∠1=90° и ∠2=30°
Решение.
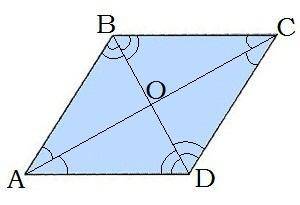
1. Найдём площадь ромба.
Площадь ромба равняется половине произведения его диагоналей.
S= ½d¹d², где d¹ и d² — диагонали ромба, а S — его площадь.
S= ½×10×24= 12×10= 120 (см²).
2. Найдём сторону ромба.
У ромба все стороны равны, кроме того, диагонали ромба пересекаются под прямым углом.
В ΔВОС: угол ВОС =90°; ВО= ½ВD= 5 см; ОС= ½АС= 12 см.
По т. Пифагора:
ВС²= BO²+OC²;
BC²= 5²+12²;
BC²= 25+144;
BC²= 169;
BC= 13 см (-13 не удовлетворяет условие задачи). => сторона ромба равна 13 см.
ОТВЕТ: 120 см²; 13 см.
И там еще рисунок во вложении понять решение.
Боковая грань правильной треугольной призмы - прямоугольник. Так как известна его диагональ, а также одна из сторон (сторона основания), по теореме Пифагора можно найти его боковую сторону, она будет равна 8. Площадь боковой поверхности будет равна 6*8*3=144, а площадь полной поверхности - 144+(36*sqrt(3)/4)*2=144+18sqrt(3) (к площади боковой поверхности прибавляем площадь верхнего и нижнего оснований - площади правильных треугольников со стороной 6).