ответ:8 см
Объяснение:
Пусть дана окружность с центром в т.О. Проведем прямую, которая пересечет окружность в т. А и т.В, т.о. АВ - хорда, АВ = 12 см. Т.к. т.А и В лежат на окружности, то ОА = ОВ = 10 см - это радиусы окружности. Получим треугольник АОВ - равнобедренный, АВ - основание. Проведем ОК ⊥ АВ, ОК - расстояние от центра до хорды. Значит ОК - медиана , АК = ВК = 12 : 2 = 6 см. Рассмотрим треугольник ОКА - прямоугольный и найдем ОК используя теорему Пифагора.
ОК² = ОА² - АК² , ОК² = 100 - 36 = 64 см², ОК = корень из 64 = 8 см
ответ: 8см
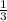BK=
. Значит, DK=2NK=2. Считаем площадь равнобедренного ADC=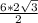
=6. Получаем, наконец, площадь полной поверхности: 3+3*6=21 (площадь основания плюс площади трех боковых граней).
. И наконец, V=9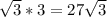
При пересечении параллельных прямых секущей образуются 4 пары равных углов.
На рисунке ∠3 - смежный ∠2 и равен 180°-∠2
∠1 и ∠2 - соответственные и, так как a||b, – равны (свойство).
∠1+∠2=2∠2
По условию ∠3=4•2∠2=8∠2
Пусть угол 2=х
Отсюда следует уравнение:
180°-х=4•2х
9х=180°, откуда х=20°
Следовательно,
∠1=∠2=20°, а
∠3=180°-20°=160°