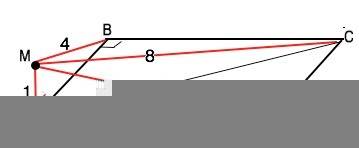
По данному условию задача может быть решена, если отрезок МА перпендикулярен плоскости прямоугольника.
Тогда МА перпендикулярна любой прямой, лежащей в плоскости АВСD.
Из прямоугольного ∆ МАВ по т.Пифагора
АВ²=MB²-MA²=16-1=15
Из ∆ МАС по т.Пифагора
АС²=MC²-AM²=64-1=63
Из ∆ АВС по т.Пифагора
ВС²=АС²-АВ²=63-15=48
АD=AB
Из ∆ МАD по т.Пифагора
MD=√(AD²+AM²)=√(48+1)=7 (см)
-------
Попробуйте более короткое решение, применив т. о 3-х перпендикулярах, по которой МВ перпендикулярна ВС
Пусть ∠М=х, тогда его внешний угол равен 180-х.
∠К=(180-х)/4.
∠М+∠К=х+(180-х)/4,
(4х+180-х)/4=100,
3х+180=400,
3х=220,
х=73.(3)°
∠М=73.(3)°, ∠К=(180-73¹/₃)/4=26²/₃=26.(6)° - это ответ.