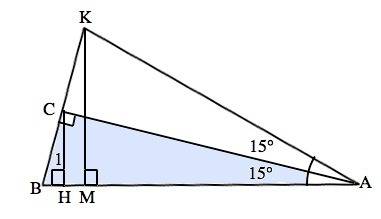
В ∆ АВС ∠ВСА=90°, ∠САК=15°
Высота СН=1. Найти АВ.
-----------
СН - высота ∆ ВСА и равна 1 по условию.
Отложим на продолжении ВС отрезок СК=ВС.
Соединим К и А.
СК=СВ, угол КСА=углу ВСА=90° (смежный).
В прямоугольных ∆ АВС и ∆ АКС катеты СК=СВ по построению, АС - общий.
∆ АСВ=∆ АСК по двум катетам =>
АК=АВ,
Треугольник АВК равнобедренный.
Угол КАС=углу САВ, следовательно, угол КАВ=2•15°=30°
Опустим перпедникуляр КМ на АВ
В прямоугольном ∆ ВКМ отрезки КС=ВС по построению. =>
С - середина отрезка ВК.
СН высота и перпендикулярна АВ, отрезок КМ перпендикулярен АВ по построению, поэтому СН║КМ, следовательно, СН- средняя линия ∆ ВКМ.=>
КМ=2СН=2.
∠КАМ=∠САВ+∠САК=30°
В прямоугольном ∆ КАМ катет КМ противолежит углу 30° и равен половине гипотенузы ( свойство).
АК=2КМ=4 ед. длины.
Гипотенуза АВ=АК=4 ед. длины - это ответ
Из треугольника ADC: Угол С=90гр., а угол ADC=60гр., за условием задачи, отсюда угол DAC=30гр., а значит катет в прямоугольном треугольнике, лежащий против угла 30гр., равен половине гипотенузы, отсюда AD=5*2=10см.
Угол ВАС=60гр., так, как угол АВС=30гр., и угол ВСА=90гр., за условием задачи.
Из треугольника BDA: угол ДАВ=60-30=30гр., так, как угол DАС=30гр., отсюда этот треугольник равнобедренный(АD=DВ), отсюда ВD=10см.
ВС=ВD+DС=10+5=15см.
ответ:15см.