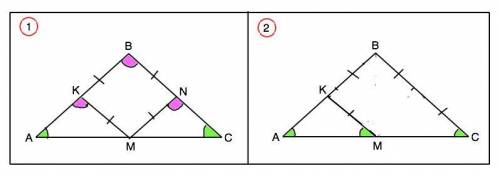
Проведем МN||АВ..
Четырехугольник КВNM - параллелограмм по построению =>
MN=ВК
Рассмотрим треугольники АКМ и СNМ
В равнобедренном треугольнике АВС углы при основании АС равны. =>
∠ВАМ=∠ВСМ
∠АКМ=∠СNМ=∠АВС - соответственные при параллельных прямых и секущей.
Если в треугольниках два угла равны, то равны е третьи углы. => ∠КАМ=∠NMC
ΔАКМ = ΔСNM по второму признаку равенства треугольников. Сходственные элементы равных треугольников равны. =>
АМ=СМ, ч.т.д.
————
Или:
КМ||ВС по условию,, ⇒∠КМА=∠ВСМ - соответственные при параллельных прямых КМ и ВС и секущей АС.
Δ АВС равнобедренный ⇒ ∠ВАС=∠ВСА, следовательно, в ∆ АКМ углы при М и А равны, ∆ АКМ - равнобедренный. КА=КМ=ВК
КМ параллельна ВС ⇒ КМ - средняя линия ∆ АВС и М - середина АС. Отсюда следует равенство АМ=МС.
Из условия -объём параллелепипеда=6 в кубе=216. АВСД-основание.Свойства ромба-сумма квадратов диагоналей=4 умноженное на а квадрат, где а=5 сторона ромба, поскольку периметр=20 а стороны ромба равны. Тогда ВД квадрат+АСквадрат=4 умноженное на 5 в квадрате.Подставим сюда соотношение ВД к АС как 3:4. Получим АС=8. Тогда ВС=3:4 умноженное на 8=6. Площадь основания (ромб) равна половине произведения диагоналей( ВД на АС ):2=(6на 8):2=24. Тогда высота параллелепипеда =объём:площадь основания=216:24=9.
Дано и рисунок, надеюсь, запишешь сам(а).
Доказательство:
1) угол NKP - острый => угол MKP - тупой
2) Рассмотрим треугольник MKP:
MKP - тупой угол (это мы доказали ранее)
угол KMP - острый
угол MPK - острый
из этого следует, что против большего угла лежит большая сторона (следствие)
=> КР < МР.