рассмотрим прямоугольный треугольник ABC в которм угол А - прямой, угол В = 30 градусам а угол С = 60.
Приложим к треугольнику АВС равный ему треугольник АВD. Получим треугольник BCD в котором B = D = 60 градусов, следовательно DC = BC. Но по построению АС 1/2 ВС, ч т д
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета равен 30 градусам.
рассмотрим прямоугольный треугольник АВC, у которого катет АС равен половине гипотенузы АС.
Приложим к треугольнику АВС равный ему треугольник ABD. Получит равносторонний треугольник BCD. Углы равностороннего треугольника равны друг другу, поэтому каждый из них = 60 градусам. Но угол DBC = 2 угла ABC, следовательно угол АВС = 30 градусов,ч т д
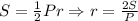
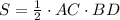
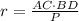
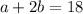- периметр треугольника.
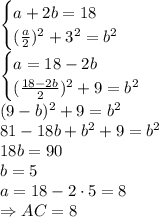
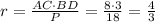
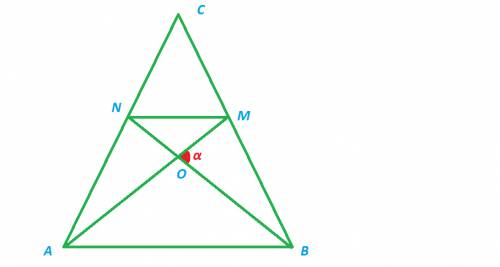
∠A и ∠A₁-прямые
BD и B₁D₁-биссектрисы .
Док-ать: ΔABC = ΔAB₁1C₁, если ∠B=∠B₁ и BD = B₁D₁
Док-во:
1) Рассмотрим Δ BDA и Δ B₁D₁A₁ Они прямоугольные.
BD=B₁D₁(по усл) и являются гипотенузами
∠ DBA=∠D₁B₁A₁(по гипотенузе и острому углу)
2) Рассмотрим Δ ABC и A₁B₁C₁
AB=A₁B₁
∠B=∠B₁ → ΔABC = ΔA₁B₁C₁(по 2-ому признаку равенств Δ)
∠A=∠A₁
ч.т.д