Трапеция - четырехугольник. В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.
Сумма длин боковых сторон данной трапеции равна сумме оснований и равна ее полупериметру.
ВС+АД=АВ+СД=120:2=60
Площадь трапеции равна произведению ее высоты на полусумму оснований ( среднюю линию)
Средняя линия равна (АД+ВС):2=30
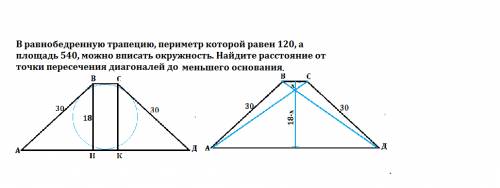
ВН и СК - высоты трапеции.
Высоту ВН трапеции найдем, разделив площадь на полусумму оснований
ВН= 540*30=18
Трапеция равнобедренная ⇒ АН=КД
Из прямоугольного треугольника АВН найдем АН:
АН=√(30²-18²)=24
ВС+НК+АН+КД=60
ВС=НК; АН=ДК
2 ВС+2*24=60
2 ВС=12
ВС=6
Треугольники, образованные диагоналями и основаниями, подобны.
Сумма их высот равна высоте трапеции =18
Пусть высота меньшего х, высота большего - 18-х
Тогда ВС:АД=х:(18-х)
6:(6+48)=х:(18-х)
Решив пропорцию, получим высоту меньшего треугольника 1,8.
Это и есть искомое расстояние.
№1
Рассмотрим треугольники FMN и FNK. Эти треугольники равны по первому признаку равенства треугольников(по двум сторонам и углу между ними). Сторона FK-общая,
сторона FM=NK, докажем это - по условию EF=EK (треугольник равобедренный), М-середина стороны EF, значит FM=1/2EF, N-середина ЕК, значит NK=1/2ЕК, значит FM=NK, а угол F=К, так треугольник FEK равнобедренный, то углы при основании равны. А так треугольники равны, то и все стороны у треугольников равны (третий признак равенства), значит сторона FN=KM
№2
В этой задачи перепроверь, что надо доказать, треугольника ЕРЕ не существует, уточни условие и я дорешаю.