Объяснение:
12
Если диагональ образует с площадью основания,то диагональ основания равна высоте прямоугольного параллелепипеда.
Найдём диагональ основания по теореме Пифагора:
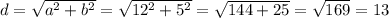
h=d=13 см
S = 2(a · b + a · h + b · h)=2(12 · 5 + 12 · 13 + 5 · 13) =2(60+156+65) = =2*281=562 см²
V=a · b · h=12 · 5 · 13=780 см³
13
Если образующая конуса наклонена к плоскости основания на 45°,то радиус основания равен высоте.Примем радиус основания за х,тогда по теореме Пифагора:
l²=2r²
12²=2x²
x²=144:2
x²=72
x=√72=6√2 см
S=π r (r + l)=π6√2(6√2+12)=π72+π72√2=π72(1+√2) см²
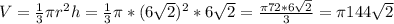
V=144√2 π см³
ответ:
v = 5√3/6 ед³.
sбок = 144 ед².
объяснение:
судя по тому, что ∠авс= 120°, параллелепипед не прямоугольный, а прямой. это "две большие разницы".
итак, высота параллелепипеда равна 9см, а в основании прямого параллелепипеда лежит параллелограмм со стороной вс = 5 см, диагональю ас=7см и углом авс = 120°. по теореме косинусов попробуем найти сторону ав.
ас² =ав²+вс² - 2·ав·вс·cos120. cos120 = -cos60 = - 1/2.
49 = ab²+25 - 2·ab·5·(-1/2) =>
ав²+5·ав -24 =0 => ab = 3cм
so = ab·bc·sin120 = 3·5·√3/2.
v = so·h = (3·5·√3/2)·9 = 5√3/6 ед³. (площадь основания, умноженная на высоту).
sбок = р·h = 2(3+5)·9 = 144 ед² ( периметр, умноженный на высоту)