Sabcd ≈ 7,5 ед.
Объяснение:
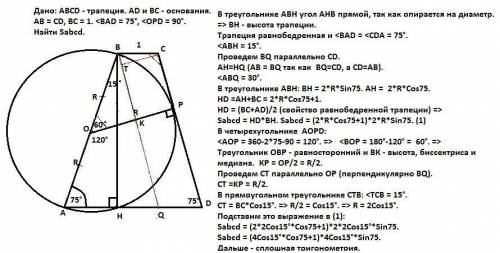
В треугольнике АВН угол АНВ прямой, так как опирается на диаметр. => ВН - высота трапеции.
Трапеция равнобедренная и <BAD = <СDА = 75°. <ABH = 15°.
Проведем BQ параллельно CD.
AH=HQ (АВ = BQ так как BQ=CD, a CD=AB). <ABQ = 30°.
В треугольнике АВН:
BH = 2*R*Sin75. АН = 2*R*Cos75. HD =AH+BC = 2*R*Cos75+1.
HD = (BC+AD)/2 (свойство равнобедренной трапеции) =>
Sabcd = HD*BH.
Sabcd = (2*R*Cos75+1)*2*R*Sin75. (1)
В четырехугольнике АОРD: <AOP = 360-2*75-90 = 120°. =>
<BOP = 180°-120° = 60°. =>
Треугольник ОВР - равносторонний и ВК - высота, биссектриса и медиана. КР = ОР/2 = R/2.
Проведем СТ параллельно ОР (перпендикулярно BQ).
CT =KP = R/2.
В прямоугольном треугольнике СТВ: <TCB = 15°.
СТ = ВС*Cos15°. => R/2 = Cos15°. => R = 2Cos15°.
Подставим это выражение в (1):
Sabcd = (2*2Cos15°*Cos75+1)*2*2Cos15°*Sin75.
Sabcd = (4Cos15°*Cos75+1)*4Cos15°*Sin75.
Дальше - сплошная тригонометрия.
Но подставив табличные значения, получим Sabcd ≈ 7,5 ед.
Если надо AD = AH+HD = 2RCos75+2RCos75+1 =
8Cos15*Cos75 +1 ≈ 3 ед.
S = 50 ед².
Объяснение:
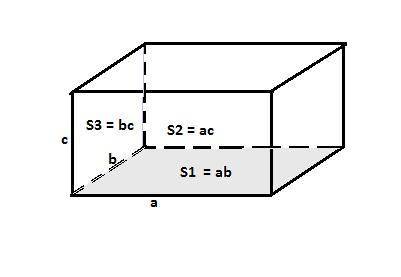
Пусть стороны прямоугольного параллелепипеда, образующие его измерения, равны "a", "b" и "c". Тогда площади основания и двух боковых граней равны
a·b = 48 (1), a·c = 40 (2) и b·c = 30 (3).
Выразим сторону b из равенств (1) и (3) и приравняем полученное:
b = 48/a и b = 30/c => 48/a = 30/c => c = 30a/48 = (5/8)a.
Подставим это значение в (2):
a·(5/8)a = 40 => a² = 320/5 = 64 => a = 8 ед.
Тогда из (1) b = 48/8 = 6 ед. c = 30/8 = 5 ед. (из 2).
Найдем по Пифагору диагональ основания:
d = √(a²+b²) = √(64+36) = 10 ед.
Площадь диагонального сечения равна:
S = d·c = 10·5 = 50 ед².
По условию, b = 8, α = 37°, γ=60°.
Тогда β = 180° - (α + γ) , тогда sin β = sin(180° - (α + γ)) = sin (α + γ)
По теореме синусов: b / sin β = c /sin γ, отсюда c = b · (sin γ / sin β)
Тогда площадь треугольника: S = 1/2 · b · c · sin α = b/2 · b · (sin γ / sin β) · sin α.
Таким образом S = (b2 · sin α · sin γ) / (2 · sin β)
S = [b2 · sin α · sin γ] / [2 · sin (α + γ)]
S = [64 · sin 37° · sin 60°] / [2 · sin 97°]
По таблице Брадиса:
sin 37° ≈ 0,602
sin 60° ≈ 0,866
sin 97° ≈ 0,993
S ≈ [64 · 0,602 · 0,866] / [2 · 0,993] ≈ 16,8
ответ ≈ 16,8