А4. 4 120°
А5. 1 10
A6. 1 16
A7. 2 6√5
А4. Угол тупой: значит 150° или 120°
S=1/2 AB*AC sin α;
3√3=1/2 *6*2sin α;
sinα=√3/2; α=120°
A5.
Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними.
угол тупой sin 150=1/2
значит α=120
или 3√3=6*2sinα/2→sinα=√3/2, α=120°
А5.
Высота, проведенная к основанию, делит его на две равные части, и косинус искомого угла становится равен половине основания, деленного на боковую сторону: cosα=b/(2a), где а- боковые стороны
√0,91=2√91/2а; а=√91/√0,91=10
A6. S=pr, де р=Р/2
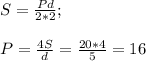
A7. Когда известны стороны ищем площадь по формуле Герона
Найдём полупериметр
р=(4+7+9)/2=10
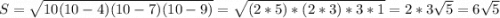
Если ты сама не напишешь дано , найти и ответ к каждой задаче- то больше не буду! Да, и формулу Герона найди и выпиши перед решением
Объяснение:
1) Дано △MPR - равносторонний, TR=8, TR-высота.
Решение: Поскольку △MPR - равносторонний, то MR=MP=PR=x. TR - высота, она же для равност. тр-ка медиана, поэтому PT=x/2. По теореме Пифагора
2) Дано ABCD - прямоугольник, AC=26, AD=10.
Решение: По теореме Пифагора находим сторону CD:
3) Дано △MNS - прямоугольный, MN=2√3, <NMS=30°.
Решение: cosNMS=
4) Дано △KEF - прямоугольный, EL - высота из вершины E, EK=9, EF=12.
Решение: По теореме Пифагора найдём
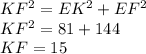
Рассмотрим △KLE. В нём sinK=x/EK=x/9. А для △KEF, sinK=EF/KF=12/15
Таким образом
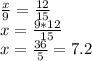

Поскольку высота треугольника делит основание пополам, то длина половины основания будет равна 12 / 2 = 6см .
Высота с половиной основания и стороной равнобедренного треугольника образует прямоугольный треугольник. Соответственно, высота основания будет равна:
h = √ 102 - 62 = √64 = 8 см
Площадь равнобедренного треугольника будет равна площади двух прямоугольных треугольников, образованных боковыми сторонами, высотой и половинами основания равнобедренного треугольника. Применив формулу площади прямоугольного треугольника, получим:
S = 6 * 8 / 2 = 24 см2
Поскольку прямоугольных треугольников два, то общая площадь равнобедренного треугольника составит:
24* 2 = 48см2 .
можно площадь найти так
S=(1/2)ah=(1/2)*12*8=48 см2 a- основание h-высота
ответ: Площадь равнобедренного треугольника составляет 48 см2