1) ∡МНО = 45
2) 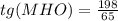
Объяснение:
Рассчитайте величину двугранного угла при основании правильной четырехугольной пирамиды если:
1.сторона основания равна 3,6 м, а высота равна 1,8 м
(ABCD-квадрат) а = 3,6
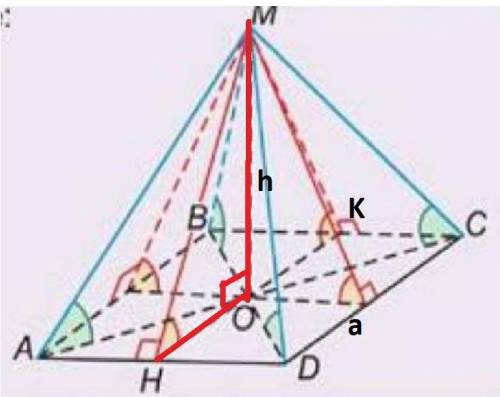
ΔMOH OH = 0.5a=1.8; OM ⊥ OH; MO= 1,8 ⇒ ΔMOH прямоугольный равнобедренный ОМ = ОН = 1,8; ∡МОН = 90° ⇒ ∡МНО = 45
2.сторона основания равна 65 см, а высота равна 99 см
(ABCD-квадрат) а = 65
ΔMOH OH = 0.5a=65/2 OM ⊥ OH; MO= 99 ⇒ ΔMOH прямоугольный ∡МОН = 90° ⇒ 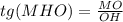
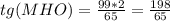
известен тангенс угла, а следовательно и сам угол при необходимости можно найти по таблицам Брадиса
У квадрата все стороны равны и его периметр составляет сумму длин всех четырех сторон или учетверенный размер одной стороны:
Р = а + а + а + а = 4 * а,
Где а - сторона квадрата.
То увеличение стороны квадрата на 25%, при условии, что фигура остается квадратом, влечет за собой увеличение всех сторон квадрата на 25% и значит, увеличивает периметр на длину одной стороны. Продемонстрируем.
Старая сторона квадрата составляла 100%, а новая составляет:
100% + 25% = 125%;
И равна:
b = а * 125 / 100 = 1,25 * а.
Новый периметр составит:
Рн = b + b + b + b = 4 * b = 4 * 1,25 а = 5 * а.
Найдем разницу периметров:
Рн - Р = 5 * а - 4 * а = а.
То есть разница между периметрами при увеличении стороны квадрата на 25% составляет длину одной стороны изначального квадрата.
Если третья сторона равна 2 см, то не выполняется неравенство треугольника. Неравенство треугольника: сумма длин любых двух сторон треугольника обязана быть больше третьей стороны, иначе такого треугольника не существует. При третьей стороне длиной 2 см, получаем
2см+2см = 4см < 19 см, и такого треугольника не существует.
Если же третья сторона длиной 19 см, то
2см+19см = 21см>19 см, и
19см+19см = 38см>2 см. И такой треугольник существует.
Периметр такого треугольника P = 19см+19см+2см = 38см+2см = 40см.