Допустим плоскости α и β параллельны, а прямая с пересекает плоскость α в точке А.
Предположим, что эта прямая не пересекается с плоскостью β. Возьмем в плоскости β точку В и проведем плоскость γ через прямую с и точку В. Плоскость γ пересекается с плоскостями α и β по параллельным прямым а и b (теорема 17.6). Но по предположению, прямая с параллельна плоскости β, а поэтому прямая с параллельна и прямой b (теорема, обратная теореме 17.3).
Получилось, что в плоскости γ через точку А к прямой b проведены две различные параллельные прямые а и с, что противоречит аксиоме. Значит предположение неверно и c пересекает β.
Параллелограмм.
CD = 12 см
AD = 3√3 см
∠ADC = 60˚
Найти:S - ?
Решение:Проведём высоту АЕ.
△DAE - прямоугольный, так как АЕ - высота.
"Сумма острых углов прямоугольного треугольника равна 90°".
=> ∠DAE = 90˚ - 60˚ = 30˚
"Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы".
=> DE = 3√3/2 см.
"Если угол прямоугольного треугольника равен 60°, то напротив лежащий катет равен произведению меньшего катета на √3".
=> AE = 3√3/2 * √3 = 9/2 = 4,5 см
S = CD * AE = 12 * 4,5 = 54 см²
ответ: 54 см²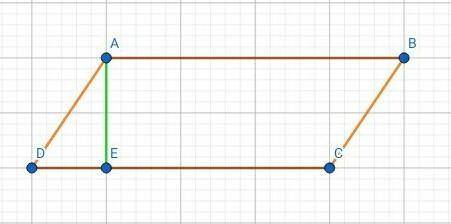
один угол 90 второй 53 и третий 37