Два бокала имеют форму конуса с одинаковой вместительностью. найдите отношение их высот, если радиус основания первого из них в два раза больше радиуса второго. ,

👇

Ответ:

пподрао

19.11.2021

Одинаковая вместительность = одинаковый объем.

Объем конуса V= 1/3 * S * H = 1/3 * π * R² * H, где S - площадь основания конуса, R - радиус основания конуса, H - высота конуса

R₁ = 2 * R₂, где R₁ - радиус основания первого конуса, R₂ - радиус основания второго конуса

Объем первого конуса V₁ = 1/3 * π * R₁² * H₁ = 1/3 * π * (2* R₂)² * H₁, где H₁ - высота первого конуса
Объем второго конуса V₂ = 1/3 * π * R₂² * H₂, где H₂ - высота второго конуса
V₁ = V₂
1/3 * π * (2* R₂)² * H₁ = 1/3 * π * R₂² * H₂
4 * R₂² * H₁ = R₂² * H₂
4H₁ = H₂
H₂ в 4 раза больше H₁ ⇒ H₁ / H₂ = 1/4

4,6(68 оценок)

Открыть все ответы

Ответ:

sirius830

19.11.2021

Рисунок без буквенных обозначений (кроме C,O,M), обозначишь, если нужно как угодно, хотя всё понятно и так.
Для удобства и быстроты всей писанины введём буквенные обозначения

-сторона основания,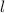

- апофема,

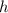- высота основания. Эти три величины потребуются для всего вычисления.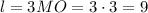
МО=3, как катет, лежащий против угла в 30°
Для Δ-ка, лежащего в основании медианы, биссектрисы, высоты совпадают, а точка их пересечения О- является центром основания.
Далее вспоминаем свойство медиан Δ-ка:
Медианы треугольника пересекаются в одной точке, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Поэтому $l=3MO=3\cdot3=9$
Теперь находим

:
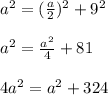
$a^2=( \frac{a}{2})^2+9^2\\ \\a^2= \frac{a^2}{4}+81\\ \\4a^2=a^2+324\\$
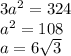
$3a^2=324\\a^2=108\\a=6 \sqrt{3}$

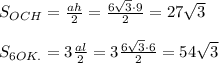
$S_{OCH}= \frac{ah}{2}= \frac{6 \sqrt{3}\cdot9}{2}=27 \sqrt{3}\\ \\ S_{6OK.}=3 \frac{al}{2}=3 \frac{6 \sqrt{3}\cdot6}{2}=54 \sqrt{3}$

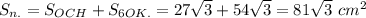
$S_{n.}= S_{OCH}+ S_{6OK.}=27 \sqrt{3}+54\sqrt{3}=81 \sqrt{3}\ cm^2$

...Ну и как "Лучший ответ" не забудь отметить, ОК?!.. ;)
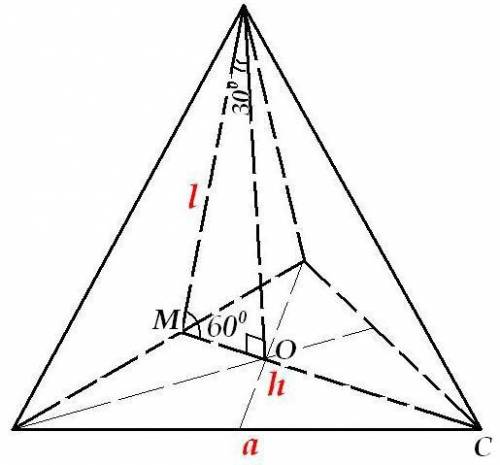
Вправильной треугольной пирамиде апофема равна 6 см, наклонена к плоскости основания под углом 60*.

Вправильной треугольной пирамиде апофема равна 6 см, наклонена к плоскости основания под углом 60*.

4,6(90 оценок)

Ответ:

4205353

19.11.2021

Основанием прямой призмы ABCKLN является равнобедренный треугольник.

Площадь грани AKLB равна 46√3 см2, угол ACB=120°, AC=CB= 18 см. Вычисли 1)площадь основания ,2) высоту призмы.

Объяснение:

1)S(осн)=S(АВС)=1/2*СВ*СА*sin∠АСВ.

S(АВС)=1/2*18*18*sin120=162*cos30°=81√3 (см²).

2) Т.к. "Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними" , то в ΔАВС

АВ²=АС²+ВС²-2*АС*ВС*cosС,

АВ²=2*18²-2*18²*cos120°,

АВ²=2*18²(1+0,5),

АВ=18√3 см.

В прямой призме боковые грани -прямоугольники ⇒S(АВКL)=АВ*ВL.

46√3=18√3*ВL или *ВL=23/9 см

4,4(77 оценок)

Это интересно:

Здоровье

05.02.2023

Как сдержать газы: 7 важных советов...

Дом-и-сад