2) 6 см 3) 38 см 4) 2 см, 4см
Объяснение:
2) Проведём из вершина другого тупого угла высоту NP. Она также отсечёт от основы MF отрезок MP=HF=2см. Значит PH=MH-MP=8-2=6см. Поскольку, проведя 2 высоты мы образовали прямоугольник PNKH, то у него NK=PH=6см
3) Т.к. AC является биссектрисой, значит <BAC=<DAC. В то же время, <DAC=<BCA как накрест лежащие при параллельных отрезках BC и AD и секущей AC. И тогда <BAC=<BCA. А значит △ABC - равнобедренный и AB=BC.
P=AB+CD+BC+AD=8+8+8+14=38см
4) Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Значит параллельные прямые a и c отсекли и на стороне AE равные отрезки AD=DE. Значит AD=2см, AE=AD+DE=2+2=4см.
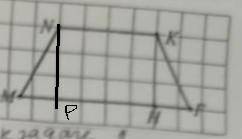
На сторонах угла∡ABC точки A и C находятся в равных расстояниях от вершины угла BA=BC. Через эти точки к сторонам угла проведены перпендикуляры AE⊥BA CD⊥BC.
1. Чтобы доказать равенство ΔAFD и ΔCFE, докажем, что ΔBAE и ΔBCD, по второму признаку равенства треугольников:
BA=BC
∡BAF=∡BCF=90°
∡ABC — общий.
В этих треугольниках равны все соответсвующие эелементы, в том числе BD=BE, ∡D=∡E.
Если BD=BE и BA=BC, то BD−BA=BE−BC, то есть AD=CE.
Очевидно равенство ΔAFD и ΔCFE также доказываем по второму признаку равенства треугольников:
AD=CE
∡DAF=∡ECF=90°
∡D=∡
Подробнее - на -
Объяснение:
∠АОВ:∠АОС=3:5 ⇒ ∠С:∠В=3:5=3х:5х.
3х+5х=120,
8х=120,
х=15,
∠В=5х=75°, ∠С=3х=45° - это ответ.