У правильной четырёхугольной пирамиды в основании лежит квадрат, а основание высота пирамиды является центром квадрата. Зная сторону квадрата (l) можно найти его диагональ - 10√2. Найдём высоту (в одном из 4 треугольников, которые образуются при пересечении диагоналей квадрата) из середины квадрата:
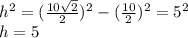
В принципе это и так логично, ведь диагональ квадрата составляет 45° с его сторонами. Теперь мы можем найти апофему пирамиды (её основание будет совпадать с основание недавно проведённой высоты т.к. это высота и медиана в равнобедренном треугольнике)
a - апофема (высота боковой грани).
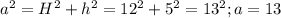
Пирамида правильная, поэтому все боковые грани равные треугольники, найдём площадь.
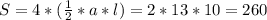
l - сторона основания.
ответ: 260 см².
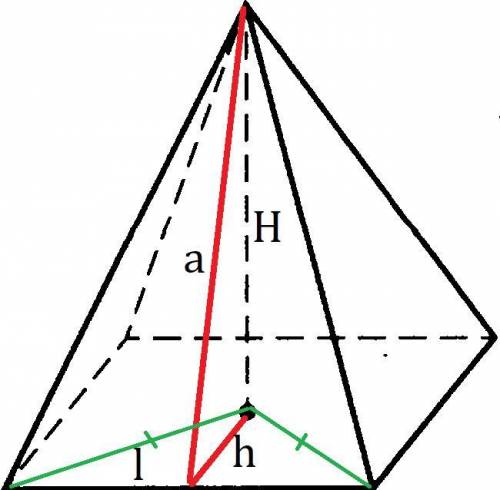
, найденный нами катет является меньшим, поэтому вращение треугольника происходит вокруг него, при этом образуется конус. Осевое сечение конуса представляет собой равнобедренный треугольник, в котором боковые стороны равны образующей, а основание равно диаметру окружности, лежащей в основании конуса, в данном случае образующая равна гипотенузе, диаметр-двум большим катетам данного треугольника, а высота-меньшему катету, значит площадь сечения равна: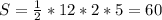
Раз график параллелен графику y = -5x + 1, то их угловые коэффициенты равны. k = -5
График y = -5x + b проходит через точку А(3; -4). Подставим эти значения и найдём b:
-4 = -5*3 + b
-4 = -15 + b
b = -4 + 15
b = 11
Запишем уравнение касательной (формулу линейной функции):
y = -5x + 11